이번 포스팅에서는 다음과 같은 함수 \(f(x)\)의 그래프를 그려보려 한다 :
\[f(x)=x^{x^{x^{x^{⋰}}}}\]
지수를 탑처럼 쌓아가는 이런형태의 연산을 흔히 ‘power tower’라 부르는데[1], \(f(x)\)와 같이 쌓아가는 그 횟수가 무한한 경우에는 ‘infinite power tower’라 부른다. 보다 간단히 기술하기 위해서 다음과 같은 표기법을 사용하기도 한다 :
\[^{1}x = x \]
\[^{2}x = x^{x}\]
\[^{3}x = x^{x^{x}}\]
\[^{n}x = x^{x^{x^{⋰ ^{x}}}} (n \text{ times})\]
\[^{\infty}x = x^{x^{x^{x^{⋰}}}}\]
과연 함수\(f(x)\)는 \(xy\)평면상에서 어떤 모양을 나타낼까? 이런모양의 함수를 처음 접했다면, 아마 ‘수렴성’에 관한 의문이 가장 먼저 들 것이다. 예를 들어 \(x\)가 \(2\)인 경우 - 즉, \(^{\infty}2\)의 값은 얼마인가? 우리가 \(n\)자리에 자연수 몇개만 넣어봐도 \(^{n}2\)의 값은 엄청난 속도로 증가한다는 것을 알 수 있다 :
| \(n\) | \(^{n}2\) |
| \(1\) | \(^{1}2 = 2\) |
| \(2\) | \(^{2}2 = 2^2=4\) |
| \(3\) | \(^{3}2 = 2^{2^{2}}=2^{4}=16\) |
| \(4\) | \(^{4}2 = 2^{2^{2^{2}}}=2^{16}=65536\) |
| \(5\) | \(^{5}2 = 2^{2^{2^{2^{2}}}}=2^{65536}\)[2] |
이정도 보면, 자연스레 ‘함수 \(^{\infty}x\)는 \(x\)가 1 보다 큰 경우 무한대로 발산하지 않을까?’싶은 생각이 들것이다. 하지만 여기서부터 반전이 시작된다. 즉, 1보다 큰 경우에도 \(^{\infty}x\)가 수렴하는 경우가 있다는 것이다.
infinite power tower에서 수렴하는 가장 대표적인 경우는 \(x\)가 \(\sqrt{2}\)일 때인데, \(^{\infty}\sqrt{2}\)의 값은 \(2\)이다 :
\[^{\infty}\sqrt{2} = \sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{⋰}}}} = 2\]
\(\sqrt{2}\)는 1.41정도의 값을 가지는 무리수이다. 1보다 큰 수에 대한 infinite power tower가 어떻게 수렴할 수 있는지 … 거기다 무리수에 대한 계산결과로 자연수가 나온다는 사실 또한 직관적으로 잘 와닿지 않을 것 같다. 하지만, \(\sqrt{2}\)에 대한 수렴성과 계산결과는 다음과 같은 한장의 그래프로 명백히 증명해 낼 수 있다 :
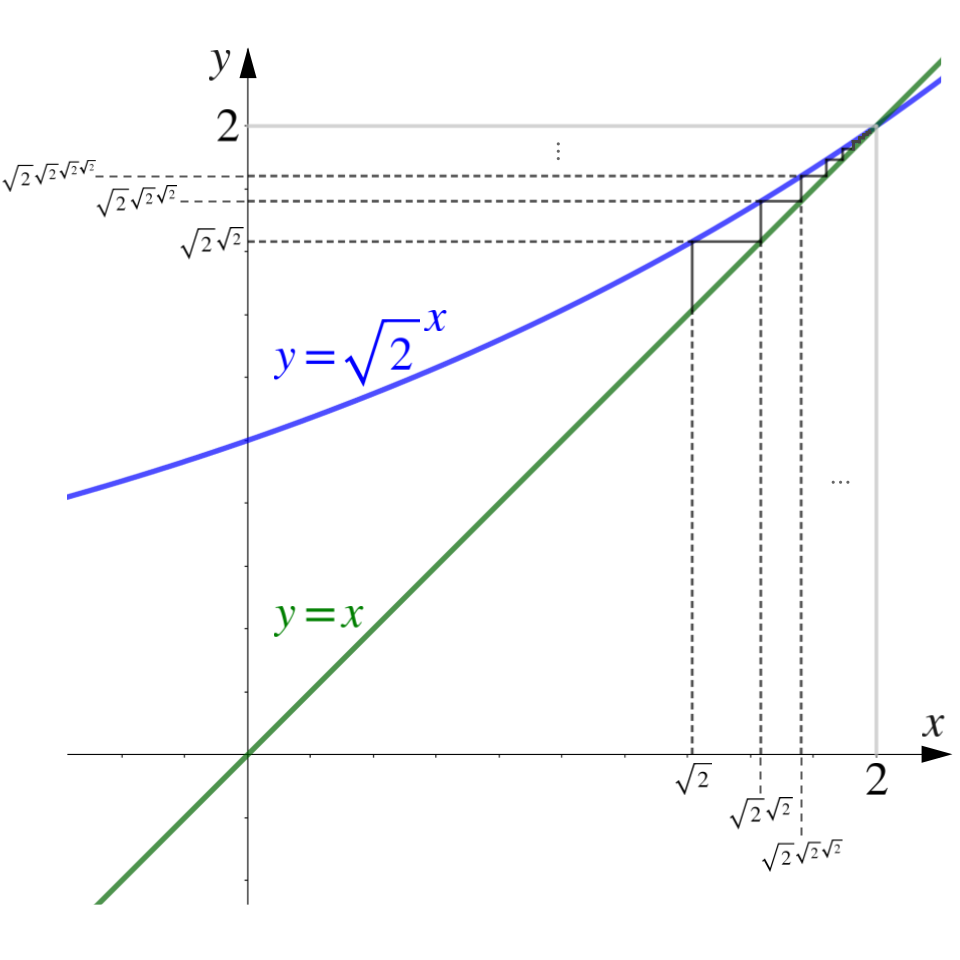
즉, \(^{n}\sqrt{2}\)의 값은 \(n\)이 1일때 약 1.41정도부터 시작하여 \(n\)이 커지면서 단조증가하는 형태를 보는데, 그 증가량이 점점 줄어들며 최종적으로는 $2$로 수렴하는 것이다. 그리고, 이러한 형태 — 즉, 지수함수 \(y=a^x\)와 직선 \(y=x\)가 두점에서 만나고 그 첫번째 교점의 \(x\)좌표가 \(a\)보다 큰 형태는 \(1 < a < e^{1/e}\)에서 항상 유지된다.
여기서 \(e^{1/e}\)의 값은 바로, \(a\)의 값이 점점 커지며 \(y=a^x\) 그래프가 점점 가팔라 지다가 직선 \(y=x\)와 접하는 순간의 \(a\)값이다. 두 그래프가 접한다는 것을 수식으로 나타내면 접점 \((x_0, x_0)\)에서 \(x_0=a^{x_0}\)와 \((a^x)’=1\)이 만족된다는 것인데, 식과 미지수가 각각 두개씩이니 풀어보면 \(a\)와 \(x_0\)의 값은 각각 \(e^{1/e}\)와 \(e\)임을 알 수 있다. \(a\)의 값이 그 이상으로 커지면 \(y=a^x\)와 \(y=x\) 그래프의 교점은 없으며, 이때 \(^{n}a\)의 값은 그래프상에서 계단형태로 급격히 올라가며 발산하게 된다. 즉, \(a\)가 \(e^{1/e}\)보다 클때 \(^{n}a\)의 값은 앞서 확인한 \(^{n}2\)와 같이 발산한다는 뜻이다. 또한 \(1 < a\)이면 \(1 < a < a^a\)이므로, 교점이 있다면 그것은 직선 \(x=a\) 보다 오른쪽에 있는 것이며, 이는 밑이 \(\sqrt{2}\)인 경우와 그 형태가 같다.
따라서, 우리는 \(1 \leq x \leq e^{1/e}\)에서 \(^{\infty}x\)의 값을 \(^{n}\sqrt{2}\)와 동일한 방법으로 찾을 수 있고, 그 범위에서 \(f(x)=^{\infty}x\)의 그래프는 다음과 같이 그려진다 :
그러면 \(x\)가 1보다 작은 경우에 대한 \(f(x)\) 그래프는 어떻게 그려질까? 복잡한 분석대신, 앞서 이용한 도식[3]을 이용하여 바로 \(^{\infty}0.5\)의 값을 구해보자 :
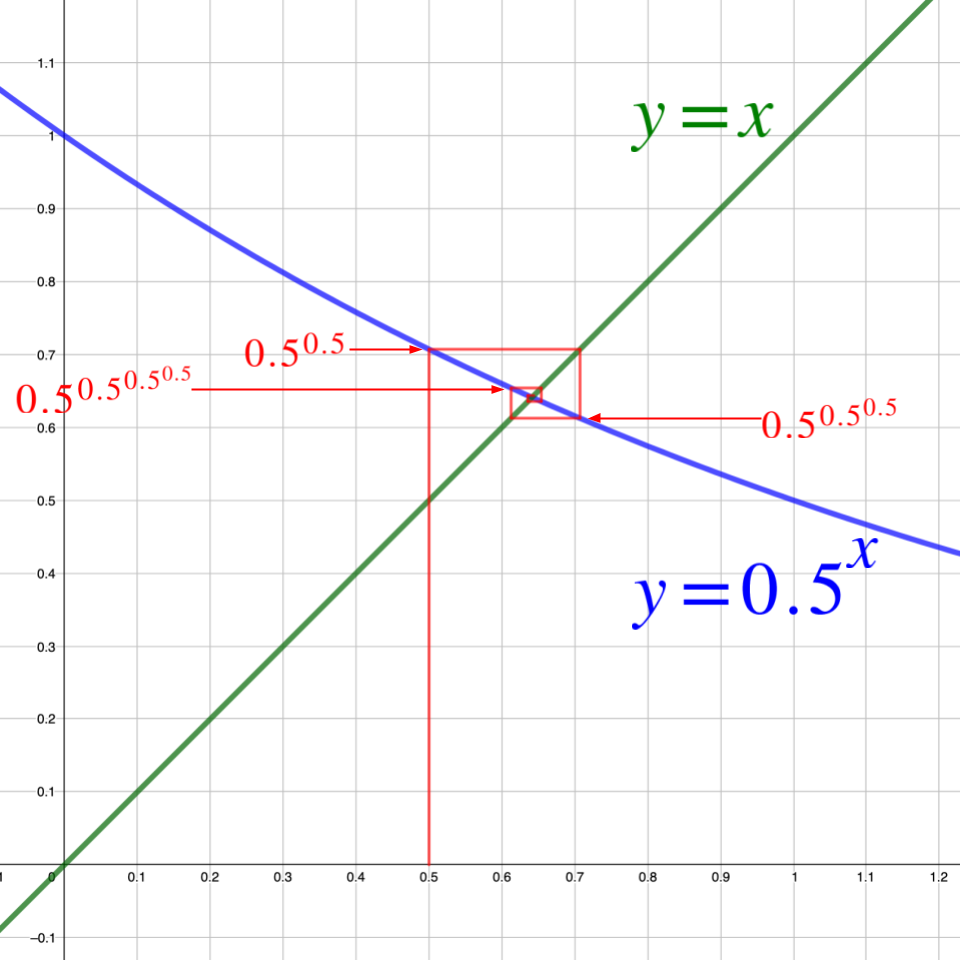
\(1 < a\)인 경우에는 교점까지 가는과정에서 지수함수 그래프가 직선보다 항상 위에 있었기 때문에 그 형태가 ‘계단식’이었다. 하지만 \(a=0.5\)인 경우에는 \(^{n}a\)에서 \(n\)이 짝수인 경우에 대해서는 지수함수 그래프가 직선보다 위에 있지만 홀수인 경우에는 아래에 있기 때문에, 직전 그래프에서처럼 ‘나선형’으로 말려들어가며 교점으로 수렴하는 형태를 보인다.
어찌되었든 \(0 < a <1\) 범위에서 \(y=a^{x}\)와 \(y=x\)는 언제나 하나의 교점을 가지며, 그것은 \(a\)가 0으로 작아짐에 따라 점점 원점을 향해서 가니, 이를 고려하면 \(0 < x < 1\)에서 \(^{\infty}x\)의 그래프는 \((0,0)\)에서 \((1,1)\)까지 단조증가하는 형태를 보일것 같다.
하지만 그렇지 않다는 것이 두번째 반전이다. \(0 < a <1\) 범위에서 \(^{\infty}a\)가 하나의 값으로 수렴하기 위해서는, \(y=a^{x}\)와 \(y=x\)의 교점에서 지수함수 기울기의 크기가 1보다 작아야 한다. 그 이유는, 그냥 기울기의 절대값이 1보다 큰 경우와 작은경우를 그려놓고 보면 직관적으로 이해 할 수 있다. 교점부위를 충분히 확대하면 지수함수가 거의 직선처럼 보일것이기 때문에[4] 그 확대된 그래프를 그려보면[5] :

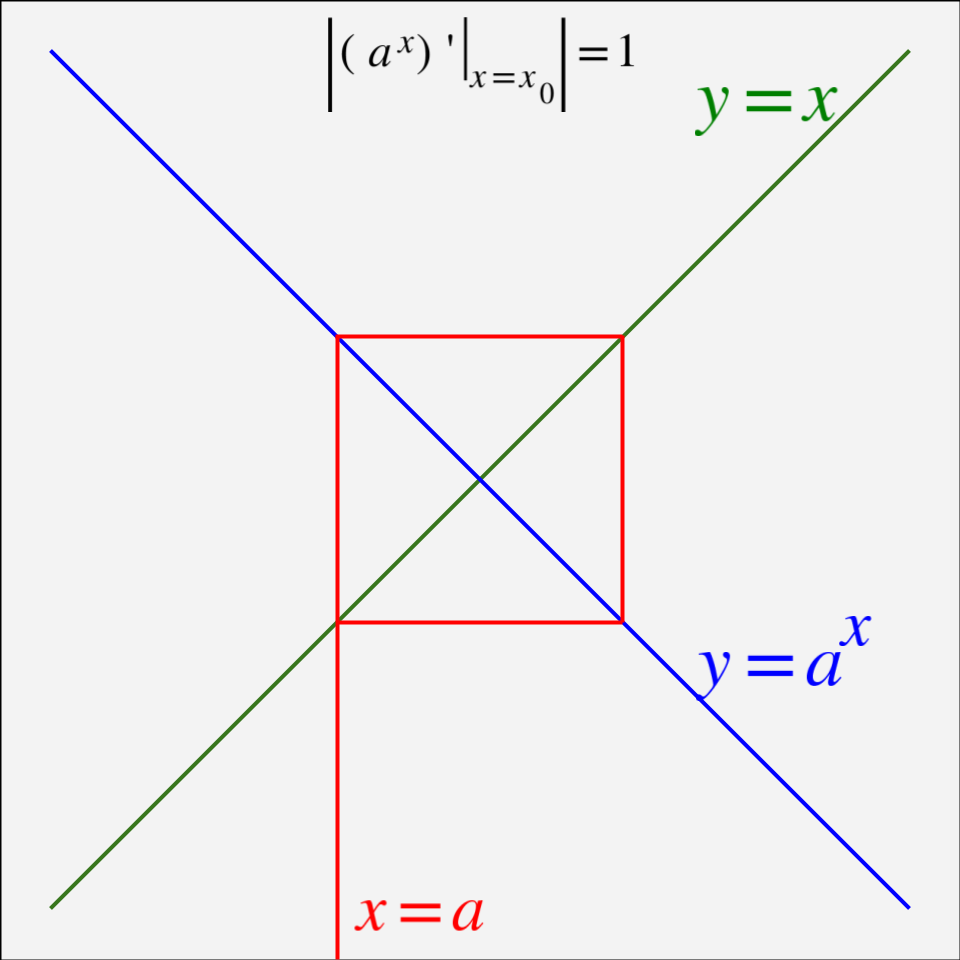

즉, \(^{n}a\)의 값들이 나선형으로 하나의 값으로 수렴하는 형태는 교점에서의 기울기 크기가 1보다 작을때만 해당되며, 기울기 크기가 1이상 일때는 \(^{n}a\)의 값이 수렴하지 않고 두 값사이를 진동한다던지 하는 다른 형태를 보인다.
따라서, \(^{\infty}x\)가 하나의 값으로 수렴하는 \(x\)값의 low limit인 \(x_0\)에서는 수학적으로 \(\left.\begin{matrix} (a^x)' \end{matrix}\right|_{x=x_0}=-1\), \(a^{x_0}=x_0\)가 만족되어야 하며, 이는 미지수와 식이 각각 두개씩이므로 풀어보면 \(x_0=1/e\), \(a=e^{-e}\)임을 알 수 있다. 앞의 upper limit까지 고려하면, 함수 \(^{\infty}x\)가 하나의 값으로 수렴하는 범위의 그래프는 점 \((e^{-e},1/e)\)에서 시작해서 \((e^{1/e},e)\)까지 이어지는 단조증가 곡선임을 알 수 있다[6] :
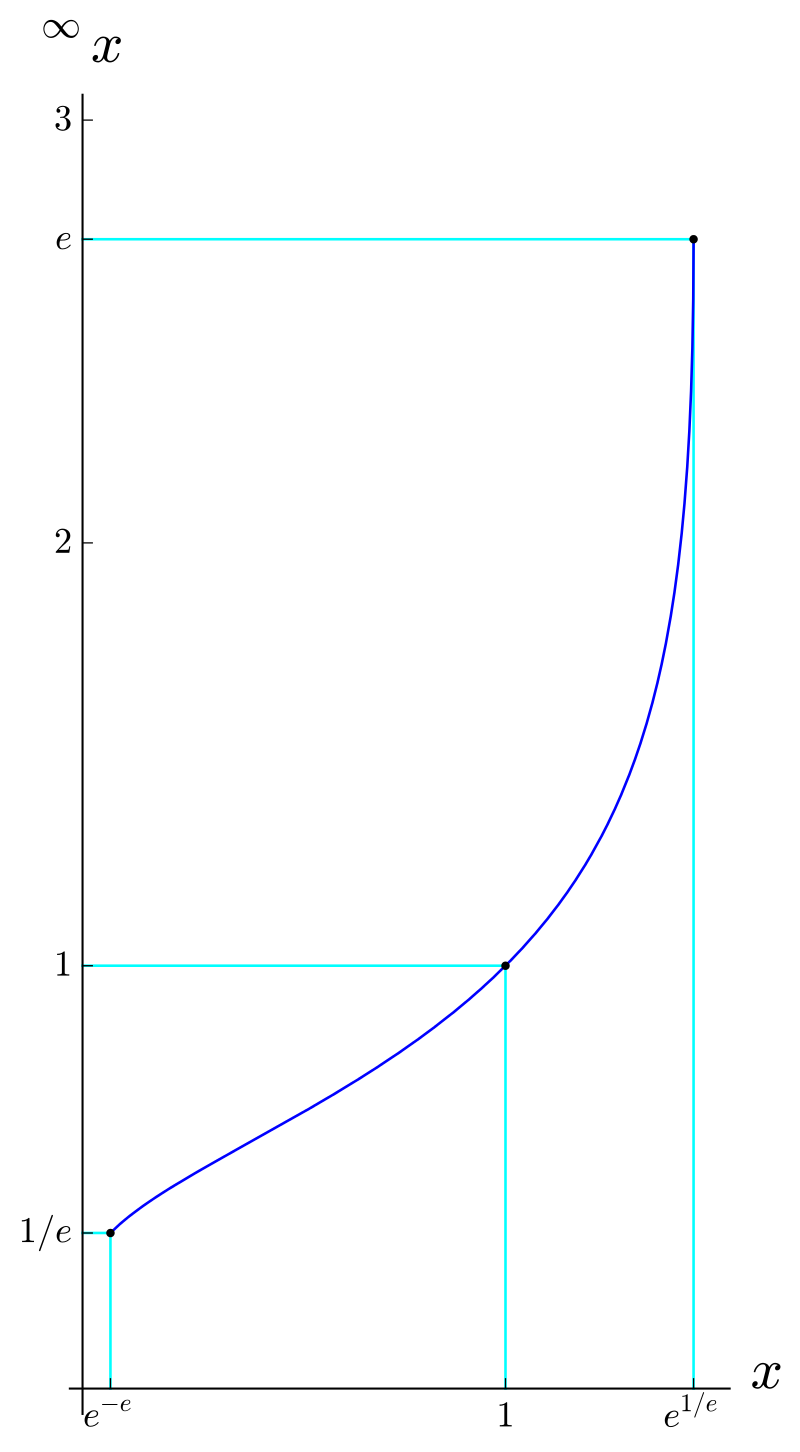
필자는 얼마전, 본인이 운영하는 학술 유튜브 채널에 이와 관련한 영상을 업로드 하였다. 그 댓글창에서는 이 \(^{\infty}x\)라는 함수가 어떤 범위에서 수렴하는지에 대한 매우 정확한 답을 적어주신 분들이 많았다. 아마도 이 글을 읽고 계신 분들도 이 정도면 함수를 다 그렸다고 생각하실지도 모르겠다. 하지만 반전은 아직 더 남아있다. \(x\)의 값을 더 내려 \(x=e^{-e}\)이하 범위에서 그래프를 그려보면, 매우 흥미로운 현상을 발견 할 수 있다. 그리고 그 내용은 상대론과 양자역학이라는 혁명 이후 — 20세기 중후반에 시작된 또다른 하나의 과학혁명[7]과 밀접하게 맞닿아 있다.
\(e^{-e}\)의 값은 약 0.066이다. 그렇다면, 그 이하의 숫자를 하나 선택해보자 — \(x\)의 값이 \(0.04\)라면, \(^{n}x\)의 값은 어떻게 될까? \(^{n}2\)의 경우처럼 양의 무한대를 향해 엄청난 속도로 발산할까? 위에서 교점에서의 기울기 크기가 1이상일때를 보면, 왠지 그 값이 양과 음을 반복하면서 발산할 것 같기도하다. 하지만 해당범위의 특정값을 넣고 막상 그래프를 그려보면, \(^{n}x\)의 값은 \(n\)이 짝수일때와 홀수일때로 나뉘어 각각 일정한 값으로 수렴한다는 것을 알 수 있다 :
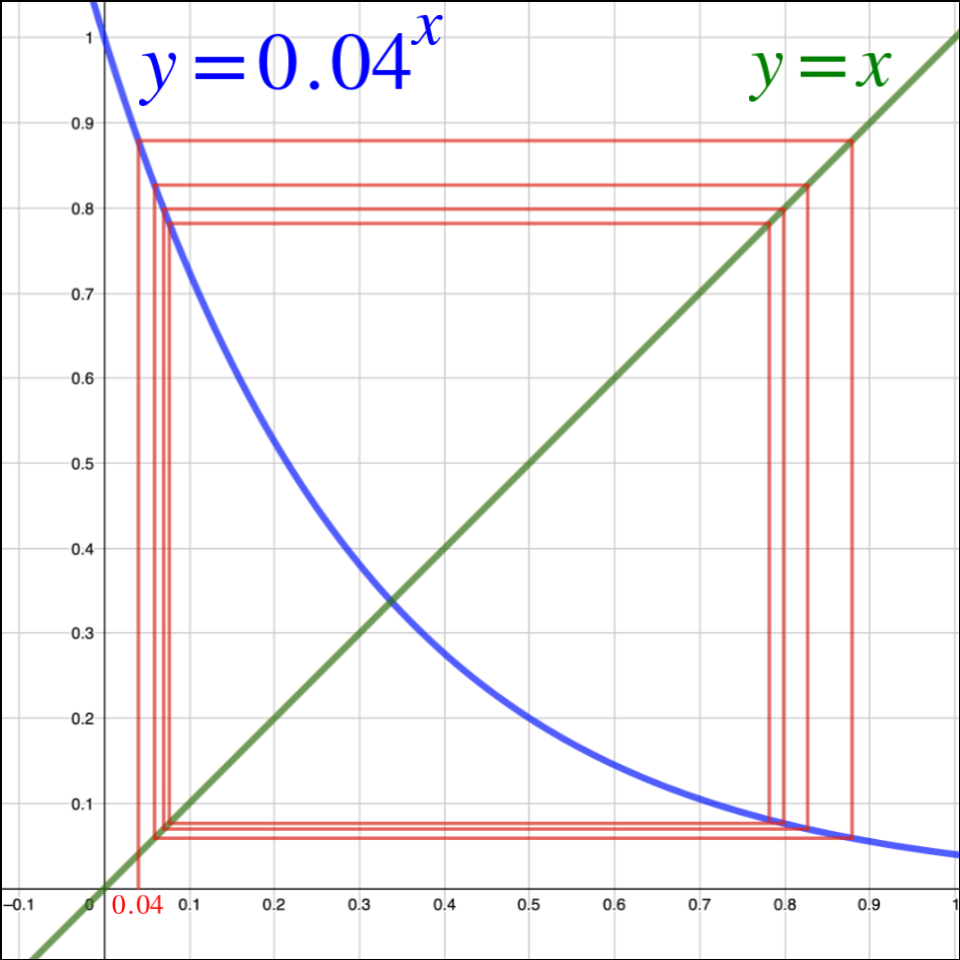
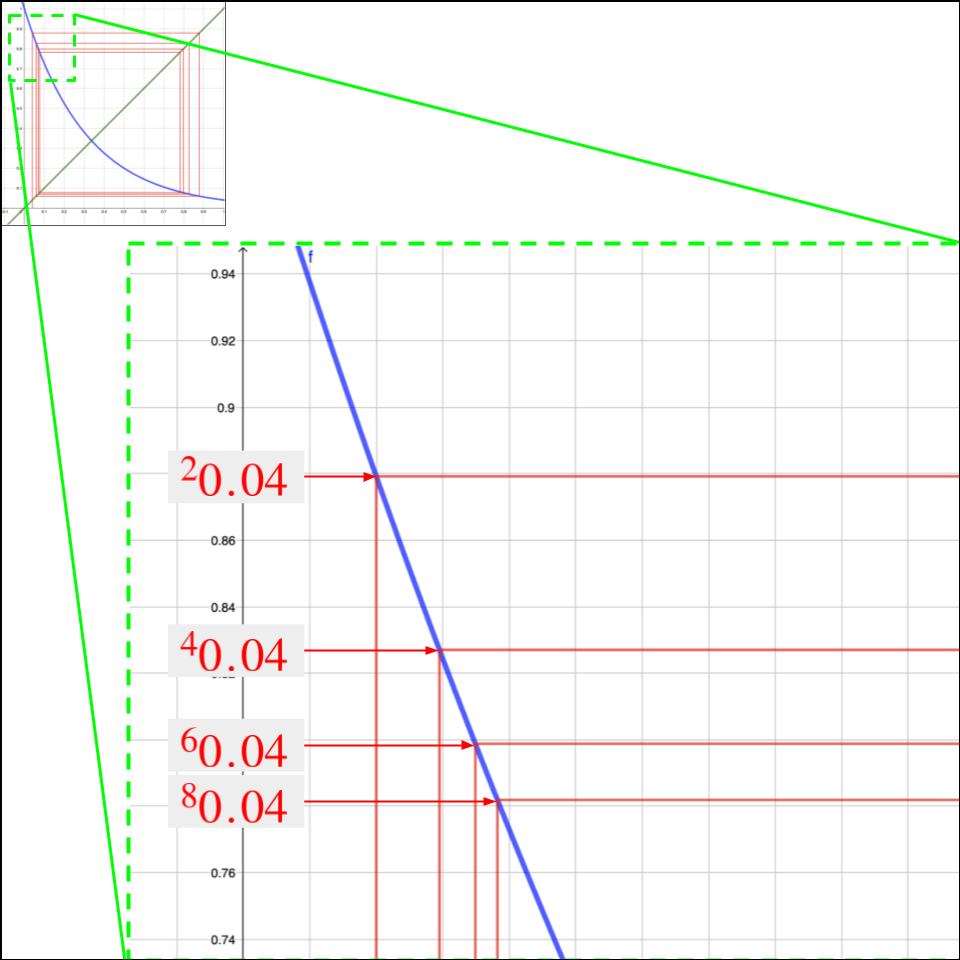
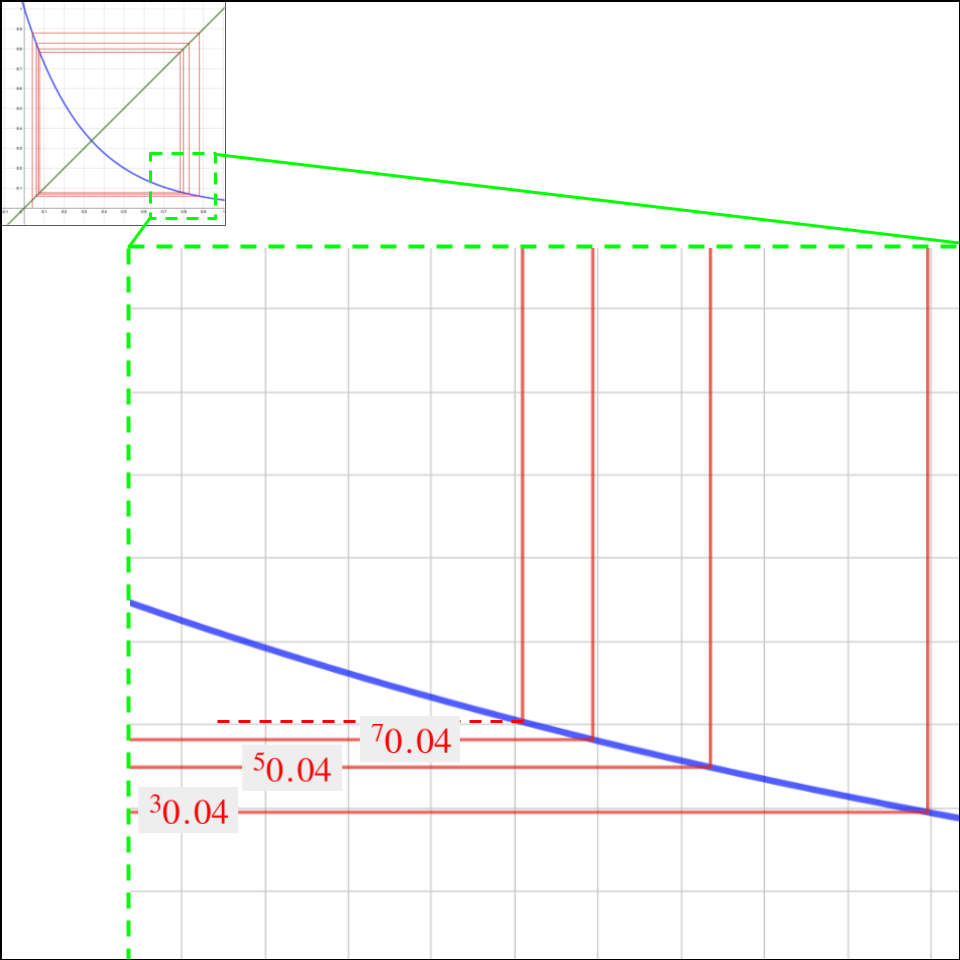
위 그래프는 \(^{n}0.04\)값들을 표시하기위해 손으로 그린거라 \(n\)의 갯수가 충분치 않은데, 프로그래밍을 통해 \(^{1000}0.04\)까지 구해보면 다음과 같은 결과를 얻을 수 있다 :
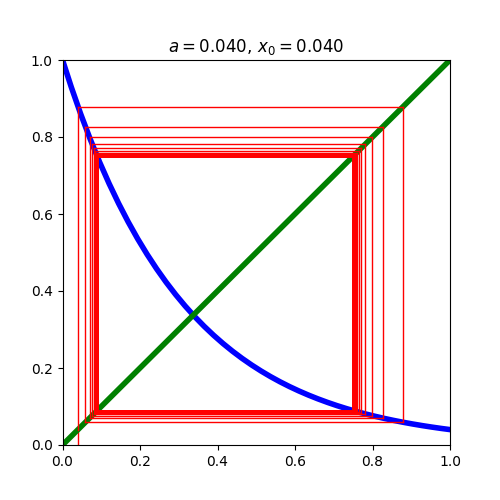
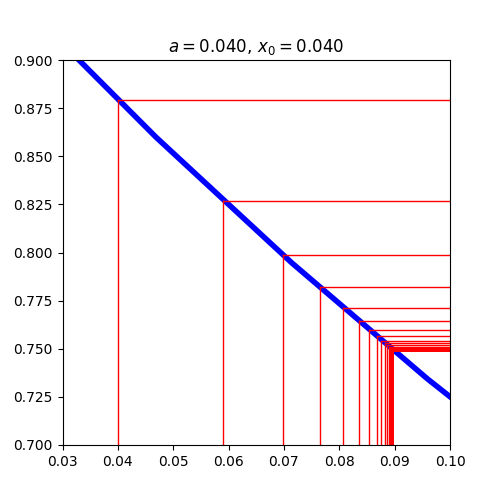
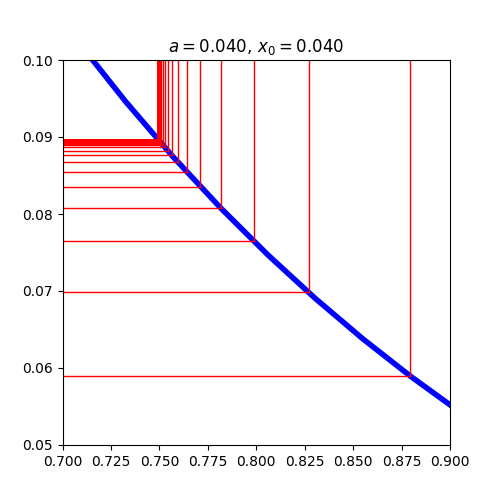
즉, 충분히 큰 \(n\)에 대해서 \(^{n}0.04\)은 두개의 값을 가진다. 짝수일경우에는 약 0.9750, 홀수일 경우에는 약 0.0046으로 수렴한다. 우리가 ‘\(^{\infty}0.04\)’라고 표기하는 것은 \(^{n}0.04\)에서 \(n\)의 값이 무한히 커지는 것을 뜻하는데, 그것은 \(n\)이 짝수일때와 홀수일때의 값을 모두 포함한다. 따라서 ‘\(^{\infty}0.04\)’의 값은 두개인 것이다.
이러한 방법을 이용하여, 우리가 앞서 구한 \(^{\infty}x\)의 범위를 \(x\)가 0일 때까지로 확장하면 어떻게 될까? 필자는 약간의 코딩을 통하여, 충분히 큰 \(n\)에 대하여 \(0 < x < e^{1/e}\)범위에서 \(^{\infty}x\)의 그래프를 그려보았다[8], [9] :

[1] 다수의 문서를 읽으면서 느낀것은, 공식적으로는 ‘power tower’ 보다는 ‘tetration’이라는 용어를 쓰는 것 같다. 보다 상세한 명명법은 관련 위키피디아 문서를 참조하시기 바란다.
[2] 이 값은 무려 19,729자리 수이다. 실제로, 아주 큰 수를 나타낼 때 power tower 형태를 이용한다고 한다.
[3] 이러한 형태의 도식을 ‘Cobweb Plot’이라한다.
[4] \(a=0.5\)인 직선그래프에서는 전체 그래프가 보일정도인데도 그 정도 영역에서도 지수함수의 곡률은 그다지 크지않다.
[5]이 그림은 수렴여부에 대한 개념설명을 위한 도식이기 때문에, 직선 \(x=a\)의 상대적인 위치는 실제와 다를 수 있다.
[6] 오일러는 이 범위를 무려 200년도 더 전인 1778년 경에 구했다고 한다. 이 결과를 보면, 프로게이머 홍진호가 만년 2등에다가 이름에도 2가 가득하다는 농담을 하곤 하는데, 오일러 (Euler)도 거의 이름과 그의 논문에 ‘e’가 가득한것 같다. 이 하나의 그래프에 \(e^{-e}\), \(e^(1/e)\), \(1/e\), \(e\)가 다 들어있는데, 마치 오일러수로 표현가능한 모든 숫자들을 나열하고있는 기분이다.
[7] ‘카오스 현상'으로 상징되기도 하는 ‘복잡계 물리'를 말한다.
[8] 본 포스팅에서는 infinite power tower에 대한 그래프를 코딩을 통해 수치적으로 그렸다. 하지만 ‘Lambert W function’이라는 함수를 이용하면 \(^{\infty}x\)에 대한 해석적 그래프를 구할 수 있다.
[9] 이와 같이, 어떠한 함수가 $x$의 값이 변하면서 2갈래로 갈라지는 현상은 ‘bifurcation’이라고 하며, 특히나 위와 같은 형태가 소리굽쇠의 모양과 비슷하다하여 ‘pitchfork bifurcation’이라 부르기도 한다.