‘무한지수탑 함수 infinite power tower function’는 대단히 신비로운 함수다. 나는 간단한 퀴즈 형식의 유튜브 영상을 만드는 과정에서 이 함수를 처음 만나게 되었는데, 그 제작과정은 자연스럽게 무한지수탑 함수에 대한 탐구로 이어졌다. 그 유튜브영상은 백만뷰를 넘으며 예상치 못한 관심을 받았다. 그 과정속에서 알게된 사실들을 통해 만든 두개의 쇼츠영상#1, #2 또한 도합 300만뷰를 넘었고, 내가 느낀 신비로움이 나만이 느끼는 무언가는 아니란 사실을 확인 할 수 있었다. 하지만 아직 그 신비로움은 끝나지 않았다. 나는 이번 포스팅을 통해 \( \sqrt{2} \)의 무한층[1] \(\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\cdot ^{\cdot ^{\cdot}}}}}\)에 대한 성질과 생각해볼 거리를 간략히 소개하려한다.
\(\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\cdot ^{\cdot ^{\cdot}}}}}\)의 값
\(\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\cdot ^{\cdot ^{\cdot}}}}}\)의 값은 얼마인가? \( \sqrt{2} \)가 1보다 크다는 사실을 생각해보면, 그것이 지수위에 지수로 무한히 쌓여 올라가면 당연히 발산할거라 생각하기 쉽다. 하지만 \(\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\cdot ^{\cdot ^{\cdot}}}}}\)의 값은 2이다. 이는 매우 비직관적인 결과처럼 보이지만, 그것을 증명하는 과정은 굉장히 직관적이고 당연하다 — 아래에 그려진 두줄의 그래프를 놓고 가만 생각해보라 :
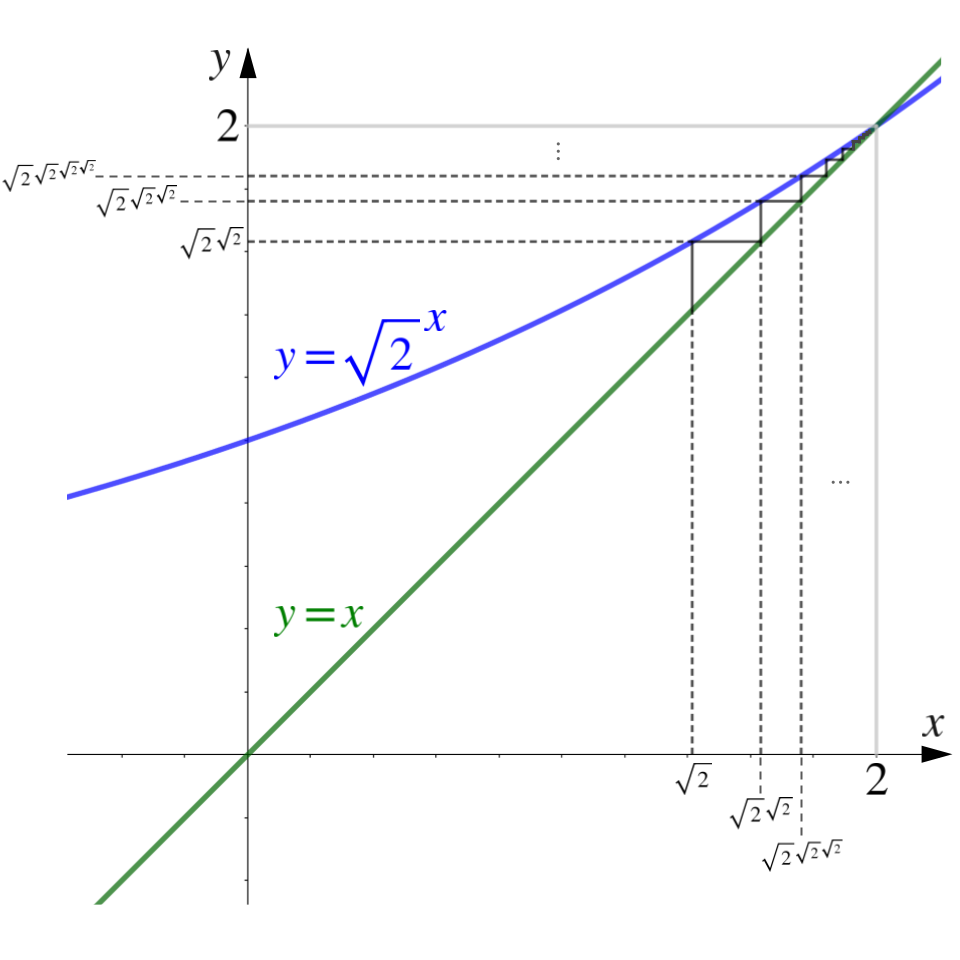
참고로 \(\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\cdot ^{\cdot ^{\cdot}}}}}\)는 그 수학적 형태 자체가 프랙탈을 품고 있다. \( \sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\cdot ^{\cdot ^{\cdot}}}}} = x \) 라 두면, 이는 \( {\sqrt{2}}^{x} \) 라 표현 될 수도 있다. \(\infty -1 \)은 여전히 \( \infty \)이며, 무한히 쌓여있는 \( \sqrt{2} \)에서 가장 아래의 한층을 빼도 그것은 여전히 무한히 쌓여있는 \( \sqrt{2} \) 다. 즉, \(\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\cdot ^{\cdot ^{\cdot}}}}}\)는 그 자체가 스스로를 포함하고 있고, 우리는 그런 자기반복적 구조를 프랙탈이라 부른다.
수식자체에 들어있는 프랙탈은 위 그래프[2]에서 기하학적 형태로도 나타난다. 위 그래프에서 (2,2) 부분을 확대하면, (2,2)를 향해 계단형태로 올라가는 형태가 무한히 계속된다. 멀리서 봤을때의 계단모양은 그 형태를 무한히 반복하며 (2,2)로 수렴하는 것이다.
함수 \(\sqrt{2}^{\sqrt{2}^{{\cdot ^{\cdot ^{\cdot^{\sqrt{2}^{x}}}}}}}\)
0.000…001의 값은 얼마인가? 중간에 무한히 많은 0이 있다면, 이 값은 0이다. 0과 0.000…001 이 같다는 사실을 달리 표현하자면, 그 둘은 어떤 방법으로도 구분될 수 없다는 말이다. 예를들어 - 이 두 숫자를 소숫점 첫째자리부터 순서대로 비교해나간다면, 소숫점 아래로 아무리 내려가도 0과 0이 서로 matching 되며 이 둘은 서로 구분되지 않는다. 따라서, 0.00…00123이든 0.00…009938474이든, 중간에 무한히 많은 0이 있다면 끝자리에 있는 어떤 유한한 수는 그 값에 영향을 주지 않는 것이다.
그렇다면 \(\sqrt{2}^{\sqrt{2}^{{\cdot ^{\cdot ^{\cdot^{\sqrt{2}^{x}}}}}}}\) 의 값은 어떨까? 위 사례를 기준으로 생각한다면, 가장 윗층에 어떤 \(x\)가 있든 상관없이 모든 \(\sqrt{2}^{\sqrt{2}^{{\cdot ^{\cdot ^{\cdot^{\sqrt{2}^{x}}}}}}}\)의 값은 같지않을까? 서로 다른 \(x\)로 끝나는 두 값을 두고 그 차이를 비교한다 해도, 그 두수를 아랫층부터 차례차례 matching 해서 올라간다면 중간에 있는 무한히 많은 \( \sqrt{2} \)의 층들로 인해 결국 그 둘은 구분 할 수 없는것 아닌가?
\(x\)에 여러 값들을 넣어보며 직접 확인해보자. 그전에 우선, \( y=x \)와 \( y=\sqrt{2}^x \)의 그래프가 (2,2)와 (4,4)에서 만나며 다음과 같은 형태를 가진다는걸 확인 할 필요가 있다 :

\(x=-1\)인 경우를 생각해보자. \(\sqrt{2}^{\sqrt{2}^{{\cdot ^{\cdot ^{\cdot^{\sqrt{2}^{-1}}}}}}}\)의 값은 cobweb plot의 시작점이 (-1,0)이란 뜻인데, 아래 그래프를 보면 그 값은 2로 수렴함을 알 수 있다 :

우리는 \(x=\sqrt{2}\)인 경우와 \(x=-1\)인 경우의 cobweb plot을 살펴봤는데, 이러한 형태는 \(x\)값이 교점 (2,2)보다 왼쪽에 있으면 항상 동일하게 나타난다. 즉, 2보다 작은 \(x\)에 대한 \(\sqrt{2}^{\sqrt{2}^{{\cdot ^{\cdot ^{\cdot^{\sqrt{2}^{x}}}}}}}\) 값은 모두 2인 것이다. \(x=2\) 일때 cobweb plot은 그 시작부터 무한히 교점 (2,2)를 향하므로 \(\sqrt{2}^{\sqrt{2}^{{\cdot ^{\cdot ^{\cdot^{\sqrt{2}^{2}}}}}}}\)의 값 역시 2이다.
\(x\)가 2보다 큰경우는 어떨까? 놀랍게도 (3,3)에서 출발한 cobweb plot은 다시 교점 (2,2)로 내려온다 :

과연 \(\sqrt{2}^{\sqrt{2}^{{\cdot ^{\cdot ^{\cdot^{\sqrt{2}^{x}}}}}}}\)의 값은 모든 \(x\)에 대해 같은 값을 가지는 것인가? 그것은 0.00…001에서 왼끝자리에 어떤 유한한 수가 들어가도 그 값이 0으로 같은것 처럼 — 그래서 그 모든수를 ‘0.000…’ 이라 표현 할 수 있는것 처럼, 모든 \(\sqrt{2}^{\sqrt{2}^{{\cdot ^{\cdot ^{\cdot^{\sqrt{2}^{x}}}}}}}\)의 값은 \(x\)에 관계없이 그 값이 2이며, 이들은 모두 \(\sqrt{2}^{\sqrt{2}^{\sqrt{2} ^{\cdot ^{\cdot ^{\cdot}}}}}\)라고 표시 할 수 있는것인가?
… 그렇지 않다. \(x=4\)일땐 \(x=2\)인 경우와 마찬가지로 cobweb plot이 그 자리에서 무한히 머물기 때문에 \(\sqrt{2}^{\sqrt{2}^{{\cdot ^{\cdot ^{\cdot^{\sqrt{2}^{4}}}}}}}\)의 값은 4이고, \(x\)가 4보다 크면 \(\sqrt{2}^{\sqrt{2}^{{\cdot ^{\cdot ^{\cdot^{\sqrt{2}^{x}}}}}}}\)는 발산한다 :

중간에 무한히 많은 0이 있다면 소숫점 아래 끝자리에 어떤 수가 있는지에 상관없이 같은값을 가지는 것과는 대조적으로, \(\sqrt{2}^{\sqrt{2}^{{\cdot ^{\cdot ^{\cdot^{\sqrt{2}^{x}}}}}}}\)의 값은 가장 윗쪽에 있는 \(x\)에 의해 결정된다. cobweb plot 기준으로 말하자면 — \( (x,0) \)은 수열의 초항과 같은 역할을 하고, \(\sqrt{2}^{\sqrt{2}^{{\cdot ^{\cdot ^{\cdot^{\sqrt{2}^{x}}}}}}}\)는 그 값이나 수렴/발산여부가 시작점에 의해 결정되는 것이다. 따라서 ‘\(\sqrt{2}^{\sqrt{2}^{\sqrt{2} ^{\cdot ^{\cdot ^{\cdot}}}}}\)’라는 표기는 오직 \( \sqrt{2} \)로 이루어진 무한 tetration 에만 써야하고, 그것이 아닌 경우에는 가장 윗층의 시작값을 명시해야만 그것이 어떤 수인지 알 수 있다.
정리하자면, 함수 \(\sqrt{2}^{\sqrt{2}^{{\cdot ^{\cdot ^{\cdot^{\sqrt{2}^{x}}}}}}}\)의 값은 모든 실수 \(x\)에 대해 다음과 같은 값을 가진다 :
$$ \sqrt{2}^{\sqrt{2}^{{\cdot ^{\cdot ^{\cdot^{\sqrt{2}^{x}}}}}}}\ = \left\{\begin{matrix} 2 & x \leq 4 \\ 4 & x=4 \\ \infty & x \geq 4 \\ \end{matrix} \right.$$
생각해보면, 이런 결과는 꽤나 놀랍게 느껴진다 — 연속적인 실수변수 \(x\)에 의해 정의되는 단일한 함수가 어떤 하나의 값을 기준으로 칼로 무자르듯 수렴/발산이 갈리는 경우를 본적 있는가? 최대 정수 함수 \(y=[x]\)는 \(x\)가 정수인 지점에서 불연속이지만, 이는 다른 어떤 기본적인 함수로 표현된것은 아니다. 분수함수 \(y=\frac{1}{x} \)는 \(x\)가 0으로 접근하면서 발산하지만, 그 형태는 부드럽고 미분가능한 형태다. 사인함수는 그러한 불연속적인 성질이 없지만, 서로 다른 파장의 사인함수를 무한히 많이 더하면 ‘사각파’나 ‘삼각파’ 같은 것들을 만들어 낼 수 있다. 하지만 그런 경우는, \(\sqrt{2}^{\sqrt{2}^{{\cdot ^{\cdot ^{\cdot^{\sqrt{2}^{x}}}}}}}\)처럼 어떤 하나의 단일한 함수로 나타낸 것이 아니라 무한히 많은 함수를 더한 결과이다. 이와관련하여 내가 아는 가장 대표적인 사례는 Fermi-Dirac distribution이다. 이는 지수함수를 통해 꽤나 간단하게 표현되는 함수인데, \(k_B T\)가 무한히 작아지면 계단처럼 완전히 불연속하게 꺽이는 step function이 된다.
\(\sqrt{2}^{\sqrt{2}^{{\cdot ^{\cdot ^{\cdot^{\sqrt{2}^{x}}}}}}}\)는 무한급수 형태도 아니고, Fermi-Dirac distribution 처럼 어떤함수의 역수를 취한것도 아닌데, 연속적인 변수 \(x\)에 대한 그래프가 어떤 하나의 지점을 기준으로 완전히 불연속적인 형태를 띈다. 이 사실은 꽤나 신비롭게 느껴지고, ‘불연속’을 만들어내기 위해선 항상 ‘무한’이 필요하다는 사실 또한 - 매우 일반적인 수학적 패턴인듯 하다.
\(\sqrt{2}^{\sqrt{2}^{{\cdot ^{\cdot ^{\cdot^{\sqrt{2}^{z}}}}}}}\)
나는 복소수를 잘 활용하면 수학을 훨씬 더 재미있게 가르칠 수 있다고 느낀다. 그것은 실용적으로도 중요하지만, 순수하게 학구적 흥미를 자극하는 목적으로 봐도 매우 훌륭한 tool이다. 해서, \( \sqrt{2} \) 무한 tetration 함수의 변수 \(x\)를 복소수 \(z\)로 바꿔보자 :
$$ \sqrt{2}^{\sqrt{2}^{{\cdot ^{\cdot ^{\cdot^{\sqrt{2}^{x}}}}}}} \to \quad \sqrt{2}^{\sqrt{2}^{{\cdot ^{\cdot ^{\cdot^{\sqrt{2}^{z}}}}}}}$$
tetration은 지수연산의 반복이다. 복소수는 지수연산에 의해 닫혀있으므로, 복소수에 대한 tetration 연산또한 닫혀있다. 따라서 \(\sqrt{2}^{\sqrt{2}^{{\cdot ^{\cdot ^{\cdot^{\sqrt{2}^{z}}}}}}}\)의 모든 정보를 표시하기 위해서는 2차원의 input과 2차원의 output — 즉 4차원이 필요하다.
2개의 2차원 복소수 평면에다 복소수의 크기와 phase를 — 또는 실수부와 허수부의 값을 특정한 colar scale로 표면해보는건 꽤나 재미있는 작업이 될 것 같다. 하지만 내가 이번 포스팅에서 보이려 하는것은 보다 더 간단한 작업 — 정의역을 수렴/발산 여부에 따라 나눠보는 것이다.
\(\sqrt{2}^{\sqrt{2}^{{\cdot ^{\cdot ^{\cdot^{\sqrt{2}^{x}}}}}}}\)는 \( x=4 \)를 기준으로 왼쪽은 수렴, 오른쪽은 발산이다. 이때, \(x\)축 상에서 수렴하는 부분을 노란색, 발산하는 부분을 파란색으로 칠한다 생각해보자. 그것은 그저 - 4를 기준으로 왼쪽은 노란색 선이, 오른쪽은 파란색 선이 그어져 있는 형태인데, 이런 형태는 그닥 흥미롭게 느껴지진 않는다.
하지만 이런 작업을 복소평면에다 해보면 상상치도 못한 놀라운 형태를 발견 할 수 있다 포스팅 아래에 코드 첨부 :

위 이미지는 실수/허수부가 각각 -10 부터 +10까지 변하는 복소평면에 대한 결과이다. 이미지의 정중앙에 가로선을 그으면, 그것이 바로 앞서 설명한 실수축에 해당한다. 실수부가 4보다 작으면 노랑, 4보다 크면 파랑인데, 이는 앞서 논했던것과 일치하는 결과이다.
어떤 컴퓨터도 연산을 무한히 할 순 없고, 위 plot은 tetration 연산을 반복하며 해당 \(z\)에서의 수렴/발산 경향이 강하게 나타날수록 그 값을 +1/0에 가깝게 부여한다. 헌데, 우리는 앞서 \(\sqrt{2}^{\sqrt{2}^{{\cdot ^{\cdot ^{\cdot^{\sqrt{2}^{x}}}}}}}\)은 어떤 하나의 값에서 수렴/발산이 매우 분명하게 갈림을 확인했다. 이러한 경향성은 위 결과가 노랑과 파랑으로 분명하게 갈린다는 사실에서도 재차 확인 할 수 있다.
앞서 무한 tetration의 수학적 형태자체가 프랙탈임을 설명했었다. 그리고 프랙탈은 다른 어떤 방향에서 봐도 어렵지 않게 찾아볼 수 있다. 앞서서는 계단형태로 올라가는 cobweb plot 속의 프랙탈 형태를 확인했었는데, 가까이서 보면 - 정의역의 수렴/발산을 가른 이 이미지 역시 프랙탈이다 :

참고로 \( z^{z^{z^{\cdot ^{\cdot ^{\cdot}}}}} \)의 정의역 역시 프랙탈이다 — 초두에 언급한 유튜브 쇼츠영상 중 하나가 이 프랙탈을 확대하는 영상이다. 사실 이런 이미지를 계산 해내는데는 상당한 computing power가 필요하다. power tower fractal를 확대하는 쇼츠영상은 1분도 안되는 길이인데도 불구하고, 그 결과를 얻기위에 맥북프로를 30시간 이상 돌려야 했다code. 나는 이 글에 이어 \(\sqrt{2}^{\sqrt{2}^{{\cdot ^{\cdot ^{\cdot^{\sqrt{2}^{z}}}}}}}\) 의 프랙탈을 확대하는 애니매이션을 해보려 한다. 독자께서도 호기심이 동한다면 이 함수로 여러가지 재미있는 계산들을 해보고 그 결과를 감상해보시기 바란다.
∷
◼︎ 복소평면 fractal code :
| import numpy as np import matplotlib.pyplot as plt # Function to check if a sequence converges def is_convergent(seq, threshold): # Check if the absolute difference between last two elements is below the threshold return np.abs(seq[-1] - seq[-2]) < threshold # Function to perform the tetration operation and check for convergence def compute_tetration_convergence(base, nx, ny, max_iter, threshold, escape_radius): # Expanding the range for real and imaginary parts x = np.linspace(4, 6, nx) y = np.linspace(-1, 1, ny) c = x[:, np.newaxis] + 1j * y[np.newaxis, :] convergence_map = np.zeros_like(c, dtype=bool) for i in range(nx): for j in range(ny): z = c[i, j] seq = [z] for k in range(max_iter): z = base ** z seq.append(z) if np.abs(z) > escape_radius or is_convergent(seq, threshold): break convergence_map[i, j] = is_convergent(seq, threshold) return convergence_map # Parameters nx, ny = 2000, 2000 max_iter = 50 threshold = 1e-5 escape_radius = 1e10 base = np.sqrt(2) # Compute the convergence map convergence_map = compute_tetration_convergence(base, nx, ny, max_iter, threshold, escape_radius) # Plotting plt.imshow(convergence_map.T, extent=[4, 6, -1, 1], origin='lower') plt.xlabel('Real part') plt.ylabel('Imaginary part') plt.title('Convergence and Divergence in Tetration with √2') plt.colorbar(label='Convergence (1) / Divergence (0)') plt.show() |
[2] 이렇게, 반복되는 수열을 어떤 함수 \(y=f(x)\)와 \(y=x\)를 오가며 이어지는 계단, 혹은 거미줄 형태의 그래프로 표현하는 방법을 ‘cobweb plot’이라 부른다.