본문 바로가기
카테고리 없음

⟪와인잔으로 배우는 양자역학⟫ 부록

the empty park 2025. 1. 29. 11:57

Contents

        ■ 부록 #1. 불확정성 원리에 대한 개념적 이해

        ■ 부록 #2. 신과 고양이가 사는 곳

        ■ 부록 #3. ‘할 수 있어야 알 수 있다’

        ■ Endnotes

 

부록 #1. 불확정성 원리에 대한 개념적 이해

물리를 제대로 배우는 과정에서 수학이 빠질 순 없습니다. 그런면에서 이번 영상의 역할은 ‘전반적인 개념을 전달하는 정도’라 할 수 있겠죠. 하지만 ‘양자역학은 기본입자의 파동적 성질을 기술한다’는 것은, 결코 가볍게 넘길 수 없는 … 영상에서 말씀드렸듯 ‘양자역학의 핵심’이라 할만한 개념입니다. 그 하나의 개념으로 얼마나 많은 내용을 이해 할 수 있는지 - 전공교재를 통해 직접 확인 해보죠.

 

영상 초반에 언급드린 양자역학 교과서 표지 뒷면에는 교과서 전체에서 추려낸 10개의 핵심공식이 정리되어 있습니다[1]:

 

이들은 크게 윗부분 다섯개와 아랫부분 다섯개로 나눌 수 있는데요 - 윗부분은, 첫번째 공식 이름에서 짐작 할 수 있듯 ‘슈뢰딩거 방정식’과 관련한 공식입니다. 영상에서 말씀드렸듯- 슈뢰딩거 방정식은 전자가 주어진 물리적 조건 하에서 어떤 정상파를 가질 수 있는지 계산 할 수 있게 해주고, 우리는 그 정상파의 선형결합으로 표현된 ‘파동함수 𝛹’를 통해 관측 가능한 모든 물리량을 계산 해 낼 수 있습니다. 이러한 슈뢰딩거식 접근방법은 ‘파동역학’이라고도 불뤼는데요 — 양자역학이란 그야말로 ‘기본입자의 파동성을 기술하는 물리이론’인 것이죠.

 

그리고 아랫쪽 다섯개는 - 6, 7번 수식이름을 보면 짐작 하시겠지만, 이들은 ‘불확정성 원리’와 관련된 수식입니다. 불확정성 원리는 양자역학에서 슈뢰딩거의 고양이 못지않게 뭔가 미스터리한 법칙인 것처럼 알려져 있지만, 사실 이 또한 파동의 일반적인 성질을 나타낼 뿐입니다.

다음과 같은 상당히 다른 형태의 두 파동을 생각해보죠 :

 

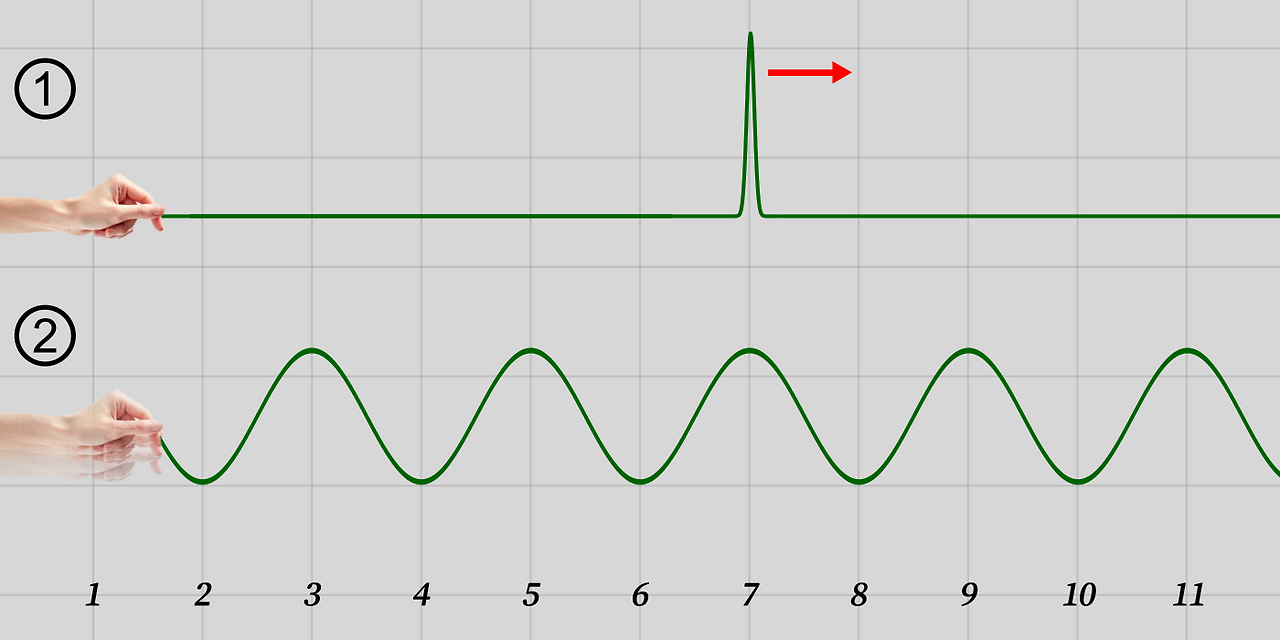
①은 일직선으로 뻗어있는 줄을 딱 한번 잽싸게 흔들어 생긴 파동이 오른쪽으로 진행하고 있는 상황이고, ②는 줄을 주기적으로 계속 흔들어서 생긴 파동입니다. 이렇게 서로 다른 두 형태의 파동 ①,②가 각각 어떤 ‘위치’와 ‘파장’을 가지는지 한번 따져볼까요?

 

파동 ①은 ‘7’을 중심으로 약 ±0.1 정도 되는 범위 속에서 좌우 대칭적으로 퍼져있습니다. 진폭이 최대가 되는 지점을 그것의 위치로 정한다면, ①의 위치는 ‘7’이 되겠죠. 그런데 ①의 ‘파장’은 어떻게 되나요? 파장이란것은, 기본적으로 공간상에서 주기적인 형태를 가지는 무언가를 기술 할 때 쓰이는 용어입니다. 그러니까 ②의 경우, 진폭이 최대가 되는 지점이 정확히 2칸마다 하나씩 나타나므로, 그 반복의 가장 작은 단위가 되는 ‘두칸’ 혹은 ‘2’가 그것의 파장이 되겠죠. 그런데 파동 ②의 ‘위치’는, 그것의 파장처럼 어떤 하나의 숫자로 표현 할 수 없습니다. 만약 파동 ②가 화면 밖 공간으로 무한히 퍼져있다면, 우리는 그 위치를 어느 한 지점으로 특정 할 수 없는 것이죠.

 

그러니까, ①은 ‘정확한 위치'를 가지고 있는 반면, 그것은 ‘파장’이라고 정의할 수 있는 어떤 주기성도 가지고 있지 않습니다. 보다 수학적으로 말하자면, 그것은 ‘위치의 부정확도는 없지만 파동의 부정확도는 무한한 상태’라 할 수 있는 것이죠[2]. 반면 ②는 ‘정확한 파장’을 가지고있지만 그것의 위치는 어떤 하나의 숫자나 특정범위로 표현 할 수 없는 … 즉, 그것은 ‘위치의 부정확도는 무한하지만 파동의 부정확도는 전혀 없는 상태’인 것입니다.

 

관심이 있으시다면, 위치와 파장 둘 다 정확한 파동을 그려보시기 바랍니다. 그것은, ‘2차원 평면위에 서로 수직하는 3개의 직선을 그어보라’는 것과 같이 근본적으로 불가능한 일입니다. 다음과 같은 예시 한가지만 살펴보죠 — 만약 ①과 같은 파동의 ‘파장’을 정확히 하기 위해서 그것을 일정한 간격으로 무한히 늘어놓아 볼까요? (아래그림에서 ①ʹ의 경우) 그런 경우, 그것의 파장은 각각의 peak가 배열된 간격으로 정확히 정의되겠지만, 되려 그것의 위치는 무한한 공간에 걸쳐 퍼지게 됩니다[3]. 그럼- ②와 같은 파동의 ‘위치’를 정확히 하기 위해 그것을 원하는 위치 근방에 압축해 놓는다면 어떻게 되죠? (아래그림에서 ②ʹ의 경우) 그렇게 되면- 그 파동의 위치는 더 많이 압축 할 수록 특정부위 근방으로 더 정확해지겠지만, 되려 그것의 주기성은 사라져버려 ‘파장’이라고 정의 할만한 특성이 완전히 없어져 버립니다.

 

어떠한 파동도 정확한 위치와  정확한 파장을 동시에 가질 수 없습니다 — 어떤 하나의 불확실성이 감소하면, 다른 하나의 불확실성은 반드시 증가하게 되죠. 이는 인간의 문제풀이 능력이 부족해서 그런게 아니라, 단지 ‘파동’이라는 물리적 대상이 가지고 있는 근본적 성질입니다.

 

이렇게 [위치, 파장]과 같이 하나가 커지면 다른 하나는 작아지는 식으로 서로 반대되는 관계를 가지는 두 물리량을 ‘상보적 관계’에 있다고 표현합니다[4]. 따라서 원자 속 전자가 파동이고, 그것이 파동의 일반적 성질을 따른다면, 전자는 당연히 상보적 관계에 있는 어떤 ‘켤레 물리량’을 가져야 합니다. 그리고 가장 대표적인 예가 바로 [위치, 운동량]이며, 그 둘 사이의 상보적관계를 기술하는 부등식을 ‘하이젠베르크의 불확정성원리’라 부르는 것이죠 (첫이미지 7번째 수식 참조).

 

이렇듯- 그것은 비록 거친 개념적 설명일 수 밖에 없었지만, ‘파동’이라는 단어는 양자역학 교과서 전체에서 추려낸 공식들을 모두 해설 해낼 수 있을정도의 강력한 핵심 키워드입니다. 하지만 안타깝게도, 그것은 양자역학의 ‘핵심’이라고 할 순 있어도 ‘전부’라고 할 순 없습니다. 양자역학에는 분명 ‘슈뢰딩거의 고양이’, ‘아인슈타인의 주사위’, ‘다중우주’, ‘확률해석’ 같은 미스터리한 면이 존재하고, 그런 문제들은 양자역학의 근본에 존재하는 어떤 ‘균열’에서 세어나오고 있습니다. 파동개념만으로는 설명 할 수 없는 … 그 양자역학의 미스터리들이 솟구쳐 나오는 ‘균열’은 대체 어디에 있는 걸까요?

 

 

부록 #2. 신과 고양이가 사는 곳

양자역학은 일반대중에게 ‘알 수 없는 우주의 미스터리’ 정도로 알려져 있는것 같습니다. 역사적인 천재들이 양자역학을 어떻게 받아들였는지 생각하면, 어쩌면 그것은 당연한 현상인지도 모르겠습니다 — 양자역학의 대표 방정식을 만든 슈뢰딩거 본인조차 그 의미를 제대로 해석하지 못해 어떤 고양이 이야기로 그것을 비판했으며, 역사상 가장 위대한 천재로 손꼽히는 아인슈타인 또한 그것을 정상적인 물리이론으로 받아들이지 않고 ‘신은 주사위를 던지지 않는다’며 양자역학을 공격했죠. 하지만 이번 영상에서는 그런 양자역학과 관련한 ‘물음표’들로 청자를 혼란에 빠뜨리는 대신, 양자역학이 자연스럽게 설명 할 수 있는 ‘느낌표’에 집중했습니다. 과연 그 양자역학의 ‘물음표’는 어디에 있는걸까요? 이번 챕터는 ‘슈뢰딩거의 고양이’와 ‘아인슈타인의 신’이 어디에 살고있는지 알아보는 시간입니다.

 

그들은 멀리있지 않습니다. 우선 먼저, 이번 영상의 키워드인 ‘파동’에 대해 다시한번 생각해보죠. 영상에서는 ‘양자화된 정상파’를 설명하기 위해 와인잔/기타줄/드럼 같은 최대한 익숙하며 시각화하기 좋은 예시들을 활용했지만, 사실 그것은 한편의 영상에 다 담지못할정도로 훨씬 더 보편적인 현상입니다. 전자기파나 음파 또한 한정된 공간속에서 양자화된 정상파를 가지며, 심지어 건물이나 다리도 그 구조에 맞는 특정한 정상파 상태를 가지죠[5].

 

… 그런데 좀 이상하지 않나요? 100년전 과학자들은 왜 이토록 흔한 현상을 곧장 활용하지 못한 걸까요? 정상파가 그토록 흔한 현상이란걸 생각하면, 100년전 과학자들이 왜 그것을 선스펙트럼에 곧장 적용하지 않고 보어원자모형같은 ‘입자형 모형’을 먼저 논했는지 … 그런 과정이, 뭔가 불필요하게 돌아돌아 가는것 처럼 보일 수도 있을 것 같습니다[6]. 하지만 그들이 익숙하게 알고있었던 또 하나의 자연현상을 고려한다면, 그것은 너무나도 자연스러운 사고의 흐름입니다[7] :

 

이것은 ‘안개상자’라는 장치 속에서 우라늄 덩어리가 알파입자를 내뿜고 있는 장면인데요 — ‘알파입자’라는것은 어떤 새로운 입자가 아니라, 중성자 2개와 양성자 2개가 모여 이루어진 원자핵입니다. 즉, 그것은 그저- 우라늄 원자핵이 붕괴되며 방출된 ‘헬륨 원자핵'인 것이죠. 그리고- 마치 비행기가 하늘에 비행운을 남기듯, 양전하를 띄는 알파입자는 극성을 띄는 알코올 분자로 이루어진 증기와 상호작용하며 눈에 보이는 자취를 남깁니다. 전자 또한 전하를 띄기 때문에 같은 원리로 알코올 분자와 상호작용 할 수 있으며, 실제로 그것은 안개상자속에 선명한 자취를 남기죠[8] :

 

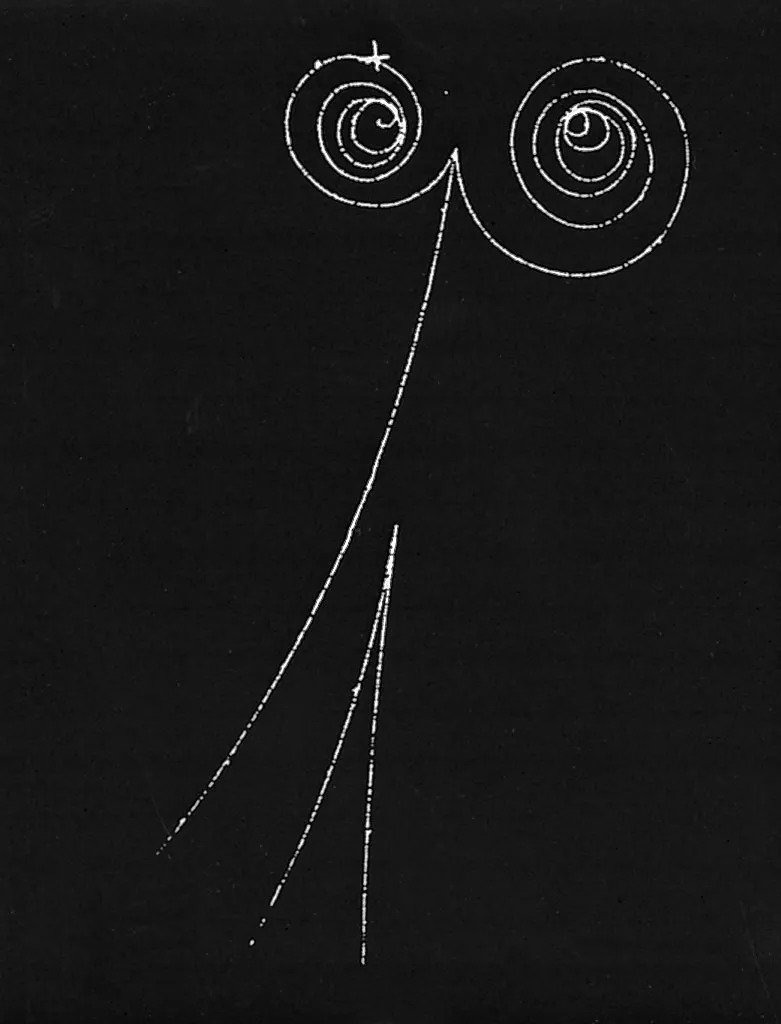
이 사진은, 일정한 자기장이 가해져있는 안개상자 속에 남겨진 양전자positron와 전자의 궤적입니다. 그것들은 서로 다른 부호의 전하를 가지기 때문에 자기장 속에서 서로 다른 방향으로 꺽이는데요, 위 사진에서 왼쪽으로 꺽이는 것이 전자의 궤적이고 오른쪽으로 꺽이는 것이 양전자의 궤적입니다. 그것의 초기속도가 빠르다면 그 관성으로 인해 꺽이는 정도가 덜 할것이고, 느린경우엔 더 급격히 꺽이며 위쪽에 보이듯 말려들어가는 궤적을 그리는 것이죠. 즉, 안개상자 속 전자는 물결이나 소리가 퍼치는것 처럼 사방팔방으로 퍼지지 않고, 명백한 입자적 거동을 보입니다. 우리는 위 궤적을 통해 그것이 특정시간에 특정위치를 지났다는 것을 알 수 있고, 따라서 안개상자 속 전자는 시공간에서 정확한 위치와 정확한 속도를 가지는 … 그것은 의심할 여지 없이 명백한 ‘입자’인 것이죠. 20세기 초 과학자들은 이러한 관측장비와 관측결과를 이미 알고 있었습니다. 그들에게 전자는 의심 할 여지 없는 ‘입자’였던 것이고, 따라서 그들은 그 지점에서부터 출발했던 것이죠.

 

… 그래서 전자는 입자인가요 파동인가요? — 전자는 원자속에서 분명 파동으로 존재합니다. 21세기에 사는 우리는 그것의 ‘사진’까지 찍을 수 있기에, 원자수준에서 전자가 파동으로 존재한다는 것은 더 이상 추상적으로 논할 일이 아닌 것이죠. 하지만 어떤 조건에서 전자는 명백한 입자로 존재합니다. 그것은 안개상자속에서 선명한 궤적을 그리고, 또 그 입자들끼리는 서로 충돌하기도 합니다. 전자가 자기장 속에서 얼마나 휠지는 뉴튼의 운동방정식으로 정확히 계산해 낼 수 있는데, 그 또한 특정 시점마다 명확한 위치와 속도를 가지는 ‘입자’에 대한 계산이며, 그 결과는 실제 실험결과를 매우 정확히 기술하죠.

 

전자는 분명 어떨땐 명백한 입자로, 또 어떨땐 명백한 파동으로 존재합니다. 그리고 양자역학의 근본적 문제점은, 바로 입자와 파동 사이 경계영역에 존재합니다. 슈뢰딩거의 고양이와 아인슈타인의 신은 ‘입자와 파동사이’에 살고 있는 것이죠.

 

입자로 존재하는 안개상자 속 전자는 고전역학 - 즉, 뉴튼의 운동법칙과 맥스웰의 전자기법칙으로 훌륭하게 기술됩니다. 또한 파동으로 존재하는 원자 속 전자는 슈뢰딩거의 방정식을 충실히 따르죠. 하지만 입자와 파동사이를 잇는 방정식은 … 없습니다. 그것은 아직까지도 우리인류에게 미스터리로 남아있습니다[9]. ‘측정의 문제’, ‘확률의 문제’ 같은 것들은 바로 그 ‘입자와 파동사이’에 존재하고, 바로 그 경계영역에 대한 불완전성이 슈뢰딩거와 아인슈타인의 비판대상이었던 것이죠[10]. 또한 그 문제에 대해선 굉장히 다양한 ‘해석’들이 존재합니다. ‘양자역학의 해석’이라는 제목의 위키피디아 문서엔 그러한 ‘해석’이 무려 15가지나 나열되어있고, ‘다중우주’라는 용어도 그 다양한 해석 가운데 등장하는 용어입니다. 서울대 물리학과 교수님이셨던 장회익 교수님은 ‘서울해석’이란 걸 내놓기도 하셨죠. 양자역학에 대해 이렇게나 많은 해석들이 존재한다는 사실은, 그것이 얼마나 불완전한 이론인지를 여실히 드러냅니다.

 

양자역학 근본에 존재하는 그런 문제들을 설명하고 논하는것은, 분명 제가 앞으로 다룰 하나의 중요한 테마가 될 겁니다. 하지만 그 또한 충분한 시간이 필요하기에, 그것은 또다른 영상이나 컨텐츠로 미루도록 하겠습니다. 대신 저는 - 그 문제자체 보단 양자역학을 바라보는 ‘엇갈린 초점’에 대해 이야기하며 이 컨텐츠를 마무리하려 합니다.

 

 

부록 #3. ‘할 수 있어야 알 수 있다’

양자역학의 ‘불완전함’이 곧 그것의 ‘쓸모없음’을 뜻하는 것은 전혀 아닙니다. 현실은 정반대입니다 — 입자-파동의 균열을 몇가지 알 수 없는 가정들로 봉합하며 완성된 현재의 양자역학[11]은 수없는 자연현상을 이해하고 수없는 발명품들을 만들어내는데 전혀 문제가 없습니다. 오히려, 대학 실험실에서 연구하는 대다수의 과학자들은 그 ‘사이공간’에 대해 그다지 궁금해하지 않습니다. 일반인 대상으로 쓰여진 양자역학 서적 중 개인적으로 인상깊게 읽은『Introducing Quantum Theory』라는 책이 있는데요 - 그 책에서 저자는 이렇게 말하고 있습니다  :

‘양자역학은 훌륭하게 작동한다. 이는 수없이 많은 문제에 대한 실질적인 답변을 준다. 양자 이론을 일상적으로 사용하는 사람들은 파동 함수가 붕괴되는 원인이 무엇인지에 대해 전혀 신경 쓰지 않는다!’

 

‘파동함수의 붕괴’라는 어려운 용어가 나오긴 했지만, 위 문장은 대분의 과학자들이 그 ‘입자와 파동사이 중간지대’에 별관심을 가지지 않는다는 사실을 말해주고 있습니다. 그들은 뉴튼과 슈뢰딩거의 방정식, 그리고 그 사이를 잇는 몇몇 가정들만으로도 이미 수없이 많은 일들을 해냈으며, 또한 수없이 많은 ‘할 수 있는 일들’과 씨름하고 있죠. 만약 여러분이 까칠한 과학자에게 확률과 측정문제에 대해 꼬치꼬치 캐묻는다면, ‘닥치고 계산이나 해보라’는 핀잔을 들을 수도 있습니다.

 

그렇게 실험실에서 연구하는 대다수의 사람들은 그 ‘경계지역’에 눈길을 주지 않습니다. 하지만 실험실 밖에 있는 이들의 시선은 오히려 양자역학의 문제와 모순에 집중되어있는 것 같습니다. 양자역학과 직접적인 관련이 없는 삶을 사는 사람들이 오히려 철학적이고 근본적인 문제에 더 큰 관심을 기울이는 이유는 분명 - 그것이 훨씬 더 흥미롭기 때문인 것 같습니다. 답이 다 나와 깨끗하게 정리되어있는 ‘선명한 무언가’ 보단 다양한 해석과 상상이 가능한 ‘흐릿한 무언가’가 더 흥미로운건 참으로 당연한 현상이겠죠? 영화 ⟪앤트맨⟫이나 ⟪인터스텔라⟫도 그렇고, 다중우주/평행우주/시뮬레이션우주 같은 소재가 수없이 많은 가사/영화/영상 등의 소재로 쓰이는것은, 양자역학의 그 ‘균열’이 그만큼 많은 해석의 가능성을 주고 인간의 호기심과 상상력을 끝없이 자극하기 때문일 겁니다. 뿐만아니라 양자역학은 우주에 존재하는 모든 기본입자와 그것들간의 상호작용을 다루기에, 그것의 불완정성은 ‘인간의 존재와 의식’, ‘우주의 시작과 끝’과 같은 거대한 질문에 대해서도 수많은 가능성을 제시합니다.

 

그런데 그런 양자역학의 결함과 그 의미를 제대로 이해하기 위해선, 양자역학 자체가 무엇을 ‘할 수 있는지’를 먼저 알아야 합니다 :

 

이것은 ‘양자역학 대표 교과서’라 말씀드린 그 책의 서문입니다. 문맥을 살려 하이라이트된 부분을 의역하자면 :

닐스보어는 양자역학에 대해 이렇게 말한다 - ‘만약 당신이 양자물리에 대해 어떤 혼란스러움도 느끼지 못한다면 당신은 그것을 제대로 이해한 것이 아니다’. 리처드 파인만 또한 이렇게 말했다 - ‘나는 양자역학을 이해한 사람은 아무도 없다고 자신있게 말 할 수 있다’

 

분명 양자역학은 수 없이 많은 상처들을 안고있다. 하지만 이 책의 목적은 그런 결함과 관련한 철학적의미에 대해 논하는 것이 아니라, ‘양자역학이 무엇을 할 수 있는지’를 가르치는 것이다. 그리고 나는, ‘양자역학이 무엇을 할 수 있는지’를 모르는 사람이 그것의 가지는 철학적 의미를 이해 할 수 있다고 생각지 않는다.

 

영상초반에, ‘슈뢰딩거의 고양이는 양자역학 교과서 말미에 딱 한페이지 나온다’고 말씀드린것 기억나시나요? 이 책은, 그만큼이나 양자역학의 결함이나 그와 관련한 해석과 철학적 문제 따위에 별 관심이 없습니다. 대신 이 책은 ‘양자역학이 어떻게 자연의 문제를 해결 할 수 있는지’에 집중하고 있죠. 그리고 저자는 독자들에게 ‘양자역학이 무엇을 할 수 있는지에 대해 모르는 사람이 양자역학 기저에 존재하는 그 문제와 의미에 대해 알 수 있다고 생각지 않는다’고 분명히 말하고 있습니다.

 

이번 영상은 이 저자가 지적하는 방향과 일치하는 선상에서 만들어졌습니다. 양자역학은 분명 불완전한 이론이지만, 그것은 결코 ‘절대 알 수 없는 우주의 미스터리’인것 만은 아닙니다. 우리는 이번 영상을 통해 ‘파동’이라는 개념이 그것의 여러가지 문제들을 일거에 해결 해 준다는것을 이해했고, 더 나아가 부록에서는 불확정성의 원리에 대한 개념적 이해에 까지 도달 할 수 있었습니다. 양자역학은 자연을 기술하는 매우 근본적인 물리법칙이고, 이것을 이해하고 대중들에게 전달하는 저의 여정은 이제 막 첫발을 내디뎠습니다. 앞으로 계속될 DMT PARK의 과학이야기에 많은 기대와 관심 부탁드리고, 또 한없이 부족한 영상과 글을 봐주셔서 대단히 감사합니다.

 

 

Endnotes

 

【References and Notes】

● Introduction to quantum mechanics … ‘양자역학 대표교과서’. 영상에 나온 책은 2판입니다.

● Radiation 2D … 전자기파 방사현상 시뮬레이션 프로그램

● Olsen, James D., and Kirk T. McDonald. "Classical lifetime of a bohr atom." Joseph Henry Laboratories, Princeton University (2005).

  • 해당 논문에서는 전자기 복사를 내는 전자는 수소원자에서 약 10-11초 (천억분의 1초)의 수명 (lifetime)을 가짐을 정량적으로 계산하였습니다.
  • 슈뢰딩거 방정식이 처음 나왔을때, 슈뢰딩거를 비롯한 많은 과학자들은 ‘𝛹’를 입자인 전자가 공간상에서 존재 할 확률이 아니라 마치 음파나 전류가 일정한 공간상에 퍼져있듯 그것이 어떤 전류같은것이 공간상에 퍼져있음을 나타낸다고 생각했습니다. 그들이 그렇게 생각한 한가지 중요한 이유는, 그것이 고전물리법칙으로 따져도 전자기복사를 내지 않았기 때문인데요 - 이 논문에서는 그런 점을 역사적맥락 속에서 보다 심도깊게 설명하고 있습니다.

● NASA’s Webb Reveals Cosmic Cliffs, Glittering Landscape of Star Birth … Jame Webb 우주망원경이 촬영한 ‘우주의 절벽’

● 중성자별 RX J1856.5-3754

  • 관련자료
  • 영상에서는 보어원자모형을 설명하기위해 태양과 비슷한 질량을 가지는 중성자별을 예시로 들어 그것들의 크기차이가 원자핵-전자와 비슷하다 설명드렸지만, 그것이 곧 먼 미래에 태양이 그런 중성자별로 붕괴함을 뜻하는 것은 아닙니다. 어떤 별이 중성자별이나 블랙홀로 중력붕괴하기 위해서는 일정질량보다 무거워야 하는데, 그 경계질량을 ‘찬드라세카 한계 (Chandrasekhar limit)’라 부르며 그 값은 대략 태양질량의 1.4배입니다.

● 스펙트럼 관련 장비

● Fraunhofer lines - Wikipedia … 태양의 선스펙트럼

● Microphone Sound Analyzer … 음파 스펙트럼 분석 프로그램

● Circular Membrane (drum head) Vibration — YouTube … 드림과 같은 원형의 2차원 표면에 생기는 정상파에 대한 실험

● Vibrations of a circular membrane - Wikipedia … 원형의 2차원 표면에 생기는 정상파는 미분방정식으로 정확한 해석적 해(analytical solution)를 구할 수 있습니다.

● Atomic orbital - Wikipedia 中, ‘Qualitative understanding of shapes’… 여기서는 원자의 오비탈을 원형의 2차원 표면에 생긴 정상파와 비교하며 그것을 개념적으로 설명하고 있습니다. 거시적인 정상파를 통해 원자의 파동적성질을 설명한다는 점에서 본 영상의 접근방법과 유사하니, 참조하시기 바랍니다.

● Hydrogen Atoms under Magnification: Direct Observation of the Nodal Structure of Stark States (PRL, 2013) … 수소원자 속 전자를 확대하여 그것의 파동함수를 관측한 2013년 PRL 논문

● 분자 오비탈

  • 동일한 두개의 원자로 이루어진 분자(Homonuclear Diatomic Molecules)는 그 구조나 정상파를 비교적 간단히 구할 수 있고, 대부분의 물리화학교재에는 그 orbital의 풀이과정과 형태가 수록되어있습니다. H2, N2, O2 같은 분자들은 기본적으로 가장 간단한 수소분자를 기준으로 문제를 푼다음 원자핵 번호를 늘려가며 확장하는 식으로 정상파와 에너지구조를 구합니다.

● ‘두 전자의 정상파가 모여 공유결합을 이룬다’는 설명에 대해서 …

영상에서는 수소분자의 정상파를 설명하기위해 ‘두 전자 각각에 해당하는 정상파가 중첩되어 새로운 형태의 안정된 정상파를 형성한다’고 설명했지만, 엄밀히 말하자면 그것은 전자하나에 대한 정상파 입니다. 입자로 존재하는 전자는 어떤 특정시점을 기준으로 하나의 특정지점에만 존재 할 수 있으나, 파동의 형태는 얼마든지 자유롭게 변할 수 있기에 하나의 전자가 두 원자핵을 감싸는 그런 형태를 가질 수 있는 것이죠. 그렇게 양성자 두개와 전자 하나로 이루어진 분자는 ‘수소분자이온 H2+’입니다. 그런데 전자는 하나의 정상파 상태에 위/아래 두개의 스핀상태가 들어갈 수 있으므로, 공간상으로는 같은 형태이지만 서로 다른 스핀상태인 전자가 하나 더해져 수소분자 H2를 이룰 수 있는거죠. 이런 스핀에 관한 규칙을 ‘파울리의 배타원리’라고 하는데, 이는 파동함수의 대칭성으로 설명 할 수 있습니다. 이러한 긴 설명이 영상에서 목표로하는 수준에 비해 너무 복잡하고, 또 공유결합 개념을 전달하는데는 오히려 영상의 설명이 더 효과적이라 판단했습니다.

● 왜 ‘구식모형’인 보어원자모형을 지금까지 쓰는가?

보어의 입자형 원자/분자모형은 그 자체에 근본적인 결함이 있고, 또 그 결함이 다른 원자모형으로 극복되었는데도 불구하고 왜 그것이 100년이 지난 지금까지 원자와 분자를 나타내는 대표모형으로 쓰이는지 의문스러운 분들이 계실 것 같습니다. 하지만 그것을 써야하는 이유는 분명합니다. 원자를 보다 사실적으로 나타내는 ‘파동형 모형’은 -  그것은 그리기도 어려울 뿐더러 내가 기술하고자 하는 원자나 분자에 몇개의 전자가 있는지를 간략하게 표현 할 수도 없습니다. 그렇다고 그것을 에너지구조 diagram에 그려넣자니 그 또한 표기의 효율성이 매우 떨어지죠. 보어 원자모형은, 비록 그것이 실제 원자와 많이 다르다 할지라도, ‘이것이 어떤 입자가 몇개 모여 만들어 졌다’는 것을 매우 직관적이고 효율적으로 표기 할 수 있게 해줍니다. 또한 수소원자나 물분자에 대한 보어모형에서 봤듯, 그것은 분자의 결합이나 구조를 나타내는데도 꽤나 효과적입니다. 개인적으로 아쉬운것은, 학교 교육과정에서는 보어원자모형 이후의 내용을 양자역학이 완성된지 100년이 지난 지금까지도 아주 피상적으로 가르친다는 겁니다. 파동형 원자모형이 그리기 어렵다거나 알아보기 어렵다해서 그 물리현상을 설명하고 이해하기가 어려운것은 아닌데 말이죠.

● Biochemistry (Voet, 4th Edition) … 광합성과 관련한 대부분의 정보는 Voet의 생화학 교재를 참조하였습니다.

● Hemoglobin … 헤모글로빈 구성분자의 에너지구조

● Heme - Wikipedia … 산소가 결합/분리되며 생기는 Heme(헤모글로빈 구성분자)의 구조변화

● Photosystem Ⅱ — YouTube … 영상제작 과정에서 알게된 영상인데, 광합성 과정 중 일어나는 전자의 이동과정이 훌륭한 애니매이션으로 시각화되어있습니다.

● 정맥/동맥 혈액간의 색상비교 — 사진(1), 사진(2)

 

【‘행성형 원자’ 시뮬레이션 관련 노트】

DMT PARK 유튜브 채널에서 ⟪멀티탭으로 배우는 양자역학⟫을 미리 보신 분들이라면, 전자기복사를 고려하지 않은 수소분자나 물분자 시뮬레이션에서 왜 이전영상에 나왔던 ‘행성계 시뮬레이션’을 사용하지 않았는지 의문이 드신 분들이 계실 것 같습니다.

 

그건- 시뮬레이션 프로그램의 기술적 문제가 있었기 때문인데요 — 이전 영상에서 사용된 ‘universe sandbox’라는 프로그램은 양성자-전자 간의 인력과 전자-전자간의 척력 까지는 가능하지만, 양성자-양성자간의 척력은 구현이 불가능 합니다. 즉- 이 프로그램은 하나의 양성자와 여러개의 전자로 구성된 ‘원자’에 대해선 타당한 ‘행성형 모형’ 시뮬레이션이 가능하지만, 양성자가 2개이상인 수소분자나 물분자를 시뮬레이션하면 양성자사이에 인력이 작용해서 옳은 결과를 주지 못합니다.

 

⟪멀티탭⟫ 영상에선 ‘네온원자’에 대한 시뮬레이션이 주였고, 수 초 가량 등장하는 물분자 시뮬레이션은 - 그저, ‘그것이 안정된 궤도를 형성하지 못한다’는 느낌만 전달하면 충분했기에 그런 하자가 있어도 괜찮았습니다. 하지만 이번 영상에서는 수소분자 시뮬레이션이 주이고, 또한 수소분자 시뮬레이션 장면에선 입자들의 구체적인 움직임까지 설명해야 했으므로, 이번 영상에서는 universe sandbox를 사용 할 수 없었습니다.

 

따라서 저는, 그러한 조건을 만족시키는 시뮬레이션을 위해 별도의 코딩을 할 수 밖에 없었는데요 - 특히나 영상에 사용된 코딩은 입자간의 충돌을 시뮬레이션 할 수 없었다는 점이 참 아쉬웠습니다. 즉, 영상에서는 ‘행성형 수소분자는 시간이 지나며 두개의 수소 분자로 나뉘어진다’고 설명 했지만, 충돌하는 경우엔 원자핵과 전자가 만나 중성자가 되는 경우도 있는 것이죠. 제가 쓴 코드는 시뮬레이션 과정에서 입자간의 충돌이 일어나면 그것을  rendering상의 오류로 인식하기 때문에, 그렇게 충돌이 일어나는 시뮬레이션 결과는 모두 제거 할 수 밖에 없었습니다. 또한, universe sandbox에서 구현되는 충돌현상은 시각적으로 매우 훌륭했고 그런 장면을 이번영상에도 활용하고 싶었는데, 기성 프로그램이라 제 마음대로 할 수 없다는 점이 참으로 아쉬웠습니다.

 

영상의 시뮬레이션은 다음의 유튜브 영상과, 해당 영상에 링크된 파이썬 코드를 활용하여 제작하였습니다 :

 

【와인잔 시연 관련 노트】

와인잔으로 소리내기

  • 영상에서 사용된 와인잔은 2~3천원 정도하는 다이소 제품입니다.
  • 어떤 와인잔이든 그 각각의 고유 진동수를 가지고 있습니다. 하지만, 영상에 제시된 방법으로 정상파가 쉽게 여기(excitation) 되는 와인잔은 따로 있습니다. 이번 경험으로 알게된 ‘소리가 잘나는 와인잔’의 몇가지 특징은 — 우선, 가능한 와인잔의 크기가 크고 입구가 넓은것이 좋습니다. 또한 와인잔의 모양은 가능한 각진 곳 없이 둥근 형태가 좋으며 와인잔벽의 두께는 가능한 얇은것이 좋습니다.
  • 와인잔을 실제 악기로 사용하는 경우도 있습니다 :

 

와인잔의 방출 스펙트럼과 관련한 몇가지 노트

와인잔에 스피커를 대고 특정 정상파를 여기 시키는 실험에서는 하나의 주파수에 대해 하나의 정상파 상태가 관측되지만, 와인잔 테두리를 문질러서 소리가 날때는 모든 상태에 대한 peak가 동시에 나타납니다. 이는, 테두리를 문질러서 여기된 와인잔의 상태는 가능한 모든 상태가 중첩된 상태라는 것이죠. 이를 수학적으로 나타내면 다음과 같습니다 : 𝛹 = a𝜓a + b𝜓b +c𝜓c + …  

 

여기서 ‘𝜓’는 각각의 스펙트럼 peak에 대응되는 - 즉, 파장이 정수개 들어가는 각각의 정상파 상태를 나타내며, ‘𝛹’'는 테두리를 문질러서 여기되는 와인잔의 정상파 상태를 나태닙니다. 즉, 𝛹는 가능한 모든 정상파 상태들이 ‘중첩’되어있는 상태입니다. 또한 그 중첩현상을 위와같이 각 정상파의 합으로 나타내는 수학적 행위를 ‘선형결합’이라 부르죠. 와인잔 스펙트럼에서 각 정상파의 peak 높이가 다르다는 것은 각각의 𝜓가 서로 다른 진폭을 가진다는 - 즉, 𝜓앞의 계수들이 서로 다른 값을 가진다는 걸 뜻합니다.

 

와인잔 흡수 스펙트럼 실험관련 참조사항

● Shattering Wineglass — Harvard Natural Sciences Lecture Demonstrations

● Wineglass Normal Modes — YouTube

  • 흡수스펙트럼 실험에 삽입된 스피커 소리는 실험영상에거 가져온게 아니라 제가 임의로 넣은 소리입니다. 실제 소리를 사용하기엔 여러가지 소음, 음질문제, 또 실제 주파수의 경우 그 소리가 너무 귀를 찌르는 듯한 느낌이 있어 청자에게 불편함을 줄 수 있는 등의 여러문제가 있었습니다. 따라서, 주파수의 변화를 확실하게 느낄 수 있는 선에서 소리의 높낮이나 크기 등을 듣기에 알맞게 조절하였습니다.

● Wine glass resonance in slow motion — YouTube

Harvard Lab에서 진행된 실험은, 비록 𝜓2와 𝜓3간의 명확한 형태차이를 보여주긴 했지만[12], 촬영 퀄리티에 대해선 상당한 아쉬움이 남는것이 사실입니다. Harvard Lab의 실험은 카메라의 frame rate를 늘려서 촬영하는 ‘slow motion’ 방식이 아닌, 일반적인 frame rate를 그대로 사용하면서도 슬로우모션 효과를 낼 수 있는 ‘Stroboscopic 효과’라는 것을 사용했습니다. 때문에 와인잔의 움직임이 충분히 부드러워 보이지 않고, 또한 촬영 setup이 정상파 형태를 잡아내는데 많이 부족하고 화질도 그다지 좋지 않습니다.

 

하지만 유튜브영상 <Wine glass resonance in slow motion>에는 고성능 촬영장비로 그러한 한계들을 극복하여 아주 훌륭한 slow motion 영상을 보여주고 있죠. 하지만 참으로 아쉬운점은, 이 영상에서 𝜓3에 대한 실험을 하지 않았다는 것입니다. slow motion 촬영장비나 주파수 조절장치는 개인이 한두번 쓸 용도로 구매하기엔 너무나 고가의 장비라 제게 언제쯤 그런 기회가 있을진 모르지만, 추후에 경제적 여건이 만족되거나 해당 장비들을 대여 할 기회가 있으면 가능한 모든 정상파 상태에 대한 영상을 촬영해 보고 싶습니다.

 

왜 파장이 4개 이상 들어가는 정상파는 관측하지 않았나?

영상에서는 스펙트럼 첫번째 선과 두번째 선이 𝜓2와 𝜓3에 대응한다는 관측결과만을 가지고 그것보다 높은 정상파 상태에 대해선 ‘𝜓N 은 N개의 파장이 들어가는 정상파 상태이다’라고 단정했습니다. 당연히 저는 그 모든 정상파들에 대한 관측결과를 보여드리고 싶었지만, 거기엔 여러가지 기술적한계가 존재합니다.

 

그 첫번째 이유는 ‘진폭’입니다. 영상에 제시된 와인잔 선스펙트럼을 보면[13], 𝜓2와 𝜓3의 소리세기는 약 -40dB 정도지만 𝜓4, 𝜓5, 𝜓6의 소리세기는 약 -60dB입니다. -40dB과 -60dB에 대한 음파에너지 차이는 100배이고 진폭의 차이는 10배인데요, 따라서 𝜓4 부터는 와인잔 진폭이 10배 정도 작아진다는 뜻입니다. 수mm 정도되는 𝜓2와 𝜓3의 진폭에서 10배정도 작아진다면, 그 울룩불룩한 정상파의 형태를 관측하는 것은 매우 어려워 질 것입니다.

 

두번째로는 𝜓3 이후의 정상파는 지속적으로 여기되지 않는다는 문제가 있는데요 — 분명 영상에 보여드린 스펙트럼은 실제 와인잔에 대한 실험결과이고, 𝜓3 이후로도 약 10개정도 되는 peak들이 관측되는 것이 사실입니다. 하지만 와인잔 소리내기를 1~2분정도 장시간 해보면, 테두리를 문지르는 처음부터 끝까지 안정적으로 존재하는 peak는 𝜓2와 𝜓3 둘 뿐 입니다. 정확한 원인은 와인잔의 3차원 구조, 마찰이 발생하는 손과 와인잔 사이의 contact 상태 등 복합적인 어떤것에 있겠지만, 결과적으로 𝜓3 이후의 상태들은 주로 소리를 내는 초기에 잠깐씩 발생하며 그것들은 안정적으로 지속되지 않습니다. 즉, 이를통해 높은 주파수의 정상파들은 그 진폭 자체도 작을뿐더러 그것을 지속적으로 여기시키는데도 어려움이 있을 거라는걸 예상 할 수 있죠. 아마 Harvard Lab에서 𝜓3 까지 밖에 실험하지 않은것은, 분명 이런 이유로 인해 그런 정상파들을 관측 할 수 없었기 때문이었던것 같습니다.

[1]  8번째 수식 ‘Canonical Commutator’와 관련한 영상이 DMT PARK 유튜브 채널에 있으니, 참조바랍니다 : ⟪양자역학에서 발견한 시뮬레이션 우주⟫

[2] 엄밀히 말하자면, ①이 가지는 파장의 불확실도는 ‘아주 크다’고 할 수는 있지만 무한하진 않습니다. ①이 파장에 대한 무한한 불확실도를 가지는 파동이 되려면, ‘7’을 기준으로 약간 퍼져있는 그 정도가 무한히 작아져야 합니다. 그런 경우 ①은, 그저 ‘7’부분에 삐죽 튀어나와있는 선분처럼 보이게 될 것이고, 우리는 그런 함수를 ‘delta function’이라 부릅니다.

[3] 이런 함수를 ‘dirac comb’라 부릅니다. 이 함수의 대표적인 적용사례는 전자가 공간상에 주기적으로 배열되어있는 원자핵에 대해 느끼는 힘을 기술하는 경우인데요, 그런 상황에서 슈뢰딩거 방정식을 풀면 고체의 에너지band 구조가 나오고, 우리는 이를통해 도체/부도체/반도체의 성질을 이해 할 수 있습니다.

[4] 닐스 보어는 ‘상보성 Complementarity’을 양자역학의 핵심개념으로 여겼습니다. 굉장히 흥미로운 한가지 사실은 - 보어는 그의 중년시절에 그 자신만의 문장(紋章, coat of arms)을 만들었는데, 그는 ‘서로 반대되는 것들은 상보적이다’는 말과 함께 그 속에 상보성을 대표하는 그림으로 태극무늬를 그려넣었습니다.

[5] 영상에서는 목소리에 대한 스펙트럼을 ‘삐죽삐죽한 선스펙트럼과는 다르다’고 표현했지만, 사실은 아기와 성인, 남과 여, 또는 개개인의 목소리가 다른이유도 서로 다른 성대구조에서 서로다른 정상파가 생기기 때문입니다. 비록 그 스펙트럼이 와인잔 스펙트럼보다는 덜 삐죽삐죽해 보일진 몰라도, 그것이 ‘성대’라는 국한된 공간에 존재하는 근육의 떨림에 의해 생겼다는 점에서 보자면 원리적으로는 와인잔과 같은 것이죠.

[6] 양자역학은 매우 근본적인 물리이론이며 또한 대단히 성공적인 이론이었던데 반해, 그것은 아주 짧은 기간 속에서 완성되었습니다. 양자역학을 만든 주요인물들이 모여 찍은 1927년 솔베이 학회 단체사진이 많은이들에게 큰 감명을 주는것은, 분명 그러한 이유 때문 일겁니다.

 

한번 생각해보시죠 — 고전역학이, 진화론이, 또는 유기화학이 만들어 지는데 몇년이 걸렸나요? 보통, 어떤 과학이론에 대한 문제제기부터 완성까지는 적어도 1세기 이상의 시간이 소요됩니다. 양자역학과 일반상대론의 통합은 그 문제가 제기된지 100년이 넘는 지금까지도 미완의 상태죠. 그런데, 현존하는 것 중 이토록 성공적이며 인류에 큰 영향을 끼친 이론이 20세기가 시작되며 막스 플랑크로 부터 출발해서 1927년 솔베이회의 즈음에 완성되기까지 불과 30여년 밖에 안되었다는 것 - 그리고 그 주역들이 한날한시에 모여 단체사진을 찍었다는건 대단히 놀라운 일입니다.

 

저는 그런 급격한 학문발전 속도에 대해, ‘당시 세계정세의 극단적 불안정성이 그런 급격한 과학이론의 발전을 가져오지 않았을까?’라는 설익은 생각을 가지고 있습니다. 20세기 앞 절반은 인류역사상 가장 큰 규모의 전쟁이었던 두차례의 세계대전이 있었습니다. 바로 그 시점이 양자역학이 만들어진 시점이고, 양자역학이 태통한 그 장소 역시 전쟁의 한복판이었던 유럽이었죠. 또한 고전물리에서 양자역학으로의 회절은 그 세계질서의 변화만큼이나 급격한 것이었습니다.

 

저는 아직 그러한 세계사나 과학사에 대해 깊이있게 논할만한 지식이 없습니다. 하지만 상당한 관심과 궁금증을 가지고 있는 주제라, 앞으로 관련한 내용을 꾸준히 읽고 공부해볼 생각입니다.

[7] 원본 유튜브영상 : Thermoelectric Cloud Chamber

[9] 이 내용을 다룬 2020년 노벨물리학상 수상자 Roger Penrose의 최근 인터뷰 내용을 첨부합니다 : Why Quantum Mechanics Is an Inconsistent Theory

[10] 과학사를 더듬어보면 - 어떤 새로운 현상을 발견하고 새로운 법칙을 찾아내는 과정 만큼이나 중요한것은 이미 알고있는 것들을 ‘통합’하는 과정인것 같습니다. 뉴튼법칙은 하늘에 떠있는 별들에 적용되는 물리법칙과 땅에서 작용하는 물리법칙을 하나로 통합했고, 아인슈타인은 시간과 공간을, 그리고 질량과 에너지를 통합했습니다. 아인슈타인은 상대론을 완성한 이후의 생을 존재하는 모든 힘을 하나의 원리로 통합하는 과정에 바쳤죠. 현인류가 마주한 자연의 큰 미스터리 역시 그런 ‘통합’과 관련되어있고, 그것들은 서로 다른 법칙이나 서로 다른 대상의 경계지점에 존재합니다 — 일반상대론과 양자역학 사이의 경계, 그리고 입자와 파동 사이의 경계가 대표적 예시라 할 수 있겠죠.

[11] 앞서 언급한 ‘양자역학의 해석’이라는 위키피디아 문서에 보면 ‘코펜하겐 해석’이라는 것이 있습니다. 이것이 바로 1927년 솔베이 회의를 즈음하여 당시 과학자들의 정리한 양자역학에 대한 해석이며, 이는 100년이 지난 지금까지도 가장 정통적인 해석으로 받아들여 집니다.

[12]편의상 ‘N개의 파장이 들어가는 정상파를 ‘𝜓N’이라 표기하겠습니다.

[13] 물론 제가 사용한 와인잔과 참조영상의 와인잔은 다른 와인잔 입니다. 크기도 어느정도 다를것이고 모양에도 약간의 차이가 있을 수 있겠죠. 하지만, 기타, 베이스, 바이올린, 첼로 등이 그 크기는 다르지만 서로 같은 형태의 정상파를 가지듯 - 유사한 형태의 와인잔들은 상당히 비슷한 스펙트럼 특성을 나타냅니다. 따라서, 와인잔 스펙트럼의 대략적인 특성을 논하는데 있어서는 영상에 등장하는 모든 와인잔이 동일하다고 생각해도 전혀 문제가 없습니다.

티스토리툴바